练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．已知直线l1：x+my+8=0与l2：（m-3）x+4y+2m=0，当m为何值时，l1与l2平行．

    分析 由平行关系可得m的方程1×4=m（m-3），解方程验证排除重合可得．

    解答 解：由题意可得1×4=m（m-3），
    解方程可得m=4或m=-1，
    经验证m=4时直线重合，应舍去
    故当m=-1时，两直线平行．

    点评 本题考查直线的一般式方程和平行关系，属基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    14．有红、黄、蓝、白4种颜色的小球，每种小球数量不限且它们除颜色不同外，其余完全相同，将小球放入如图所示编号为1，2，3，4，5的盒子中，每个盒子只放一只小球．
    （1）放置小球满足：“对任意的正整数j（1≤j≤5），至少存在另一个正整数k（1≤k≤5，且j≠k）使得j号盒子与k号盒子中所放小球的颜色相同”的概率；
    （2）记X为5个盒子中颜色相同小球个数的最大值，求X的概率分布和数学期望E（X）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．函数y=xlnx在区间（　　）
    A．（0，+∞）上单调递减B．$（\frac{1}{e}，+∞）$上单调递减C．$（0，\frac{1}{e}）$上单调递减D．（0，+∞）上单调递增

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．若A，B，C，D，E，F六个不同元素排成一列，要求A不排在两端，且B、C相邻，则不同的排法共有144种（用数字作答）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．曲线$\left\{\begin{array}{l}x=3-4t\\ y=1-3t\end{array}$（t为参数）与曲线ρ=1交点个数（　　）
    A．0B．1C．2D．以上都有可能

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．在△ABC中，点D在线段BC上，且满足BD=$\frac{1}{2}$DC，过点D的直线分别交直线AB，AC于不同的两点M，N，若$\overrightarrow{AM}$=m$\overrightarrow{AB}$，$\overrightarrow{AN}$=n$\overrightarrow{AC}$，则（　　）
    A．m+n是定值，定值为2B．2m+n是定值，定值为3
    C．$\frac{1}{m}$+$\frac{1}{n}$是定值，定值为2D．$\frac{2}{m}$+$\frac{1}{n}$是定值，定值为3

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知曲线C：y=x+$\frac{1}{x}$
    （1）求证：曲线C上的各点处的切线的斜率小于1；
    （2）求曲线C上斜率为0的切线方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知圆C过点p（1，1），且与圆M：（x+2）2+（y+2）2=r2（r＞0）关于直线x+y+2=0对称．
    （1）求圆C的方程．
    （2）过点P作两条相异直线分别与圆C相交于A，B，且直线PA和直线PB的倾斜角互补，O为坐标原点，求证：直线OP与直线AB平行．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

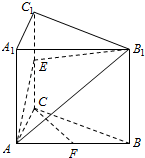    8．如图，在直三棱柱ABC-A1B1C1中，∠ACB=90°，E是棱CC1上的动点，F是AB中点，AC=BC=2，AA1=4．
    （Ⅰ）求证：CF⊥平面ABB1；
    （Ⅱ）试确定点E的位置，使得CF∥面AEB1．

    查看答案和解析>>

    同步练习册答案