
已知a=(1,2),b=(-2,n) (n>1),a与b的夹角是45°.
(1)求b;
(2)若c与b同向,且a与c-a垂直,求c.
(1) b=(-2,6) (2) (-1,3).
【解析】
试题分析:(1)利用向量夹角公式可得关于n的方程,解出n即得向量b;
(2)由c与b同向,同向,可设c=λb (λ>0),利用向量垂直的充要条件可求得λ,代入即可求得c;
(1)a·b=2n-2,|a|=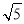 ,|b|=
,|b|=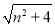 ,
,
∴cos 45°=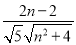 =
=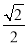 ,∴3n2-16n-12=0,∴n=6或n=-
,∴3n2-16n-12=0,∴n=6或n=-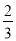 (舍),∴b=(-2,6).
(舍),∴b=(-2,6).
(2)由(1)知,a·b=10,|a|2=5.又c与b同向,故可设c=λb (λ>0),(c-a)·a=0,
∴λb·a-|a|2=0,∴λ=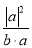 =
=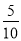 =
= ,∴c=
,∴c=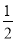 b=(-1,3).
b=(-1,3).
考点:平面向量数量积的运算;利用数量积判断两向量的垂直关系.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源:2016届安徽省高一第二学期第一次月考数学试卷(解析版) 题型:选择题
函数 的定义域是 ( )
的定义域是 ( )
A.(-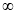 ,-1) B.(1,+
,-1) B.(1,+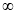 ) C.(-1,1)∪(1,+
) C.(-1,1)∪(1,+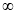 ) D.(-
) D.(-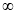 ,+
,+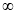 )
)
查看答案和解析>>
科目:高中数学 来源:2016届安徽省高一下学期期中考试数学试卷(解析版) 题型:选择题
△ABC的内角A、B、C的对边分别为a、b、c.若a、b、c成等比数列且c=2a,则cos B= ( )
A.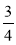 B.
B.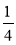 C.
C.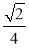 D.
D.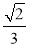
查看答案和解析>>
科目:高中数学 来源:2016届安徽省高一下学期期中考试数学试卷(解析版) 题型:解答题
设不等式组 所表示的平面区域为
所表示的平面区域为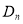 ,记
,记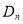 内的格点(格点即横坐标和纵坐标均为整数的点)个数为
内的格点(格点即横坐标和纵坐标均为整数的点)个数为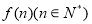
(1)求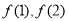 的值及
的值及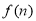 的表达式;
的表达式;
(2)设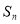 为数列
为数列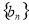 的前
的前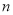 项的和,其中
项的和,其中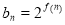 ,问是否存在正整数
,问是否存在正整数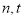 ,使
,使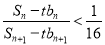 成立?若存在,求出正整数
成立?若存在,求出正整数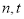 ;若不存在,说明理由
;若不存在,说明理由
查看答案和解析>>
科目:高中数学 来源:2016届安徽省高一下学期期中考试数学试卷(解析版) 题型:选择题
已知等差数列{an}的公差d≠0,若a5、a9、a15成等比数列,那么公比为 ( )
A.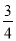 B.
B.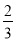 C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2016届安徽省高一第二学期第一次月考数学试卷(解析版) 题型:选择题
等差数列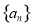 中,a1=1,d=3,an=298,则n的值等于( )
中,a1=1,d=3,an=298,则n的值等于( )
A.98 B. 100 C.99 D.101
查看答案和解析>>
科目:高中数学 来源:2016届安徽池州一中、铜陵三中高一重点班测试文科数学卷(解析版) 题型:选择题
△ABC的内角 、
、 、
、 的所对的边
的所对的边 、
、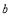 、
、 成等比数列,且公比为
成等比数列,且公比为 ,则
,则 的取值范围为( )
的取值范围为( )
A.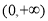 B.
B.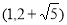 C.
C. D.
D.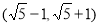
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com