
| 6 |
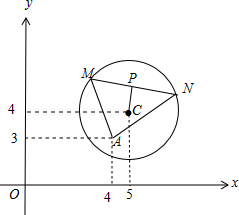
| (x-4)2+(y-3)2 |
| CN2-CP2 |
| (x-4)2+(y-3)2 |
| 6-[(x-5)2+(y-4)2] |


 特高级教师点拨系列答案
特高级教师点拨系列答案 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:
| m |
| n |
| 3 |
| 1 |
| 2 |
| m |
| n |
| m |
| 3 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| (sin2a) |
| (cos2a) |
| kπ |
| 2 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:
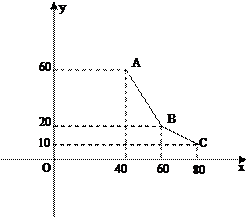 小张经营某一消费品专卖店,已知该消费品的进价为每件40元,该店每月销售量y(百件)与销售单价x(元/件)之间的关系用如图的一折线表示,职工每人每月工资为1000元,该店还应交付的其它费用为每月10000元.
小张经营某一消费品专卖店,已知该消费品的进价为每件40元,该店每月销售量y(百件)与销售单价x(元/件)之间的关系用如图的一折线表示,职工每人每月工资为1000元,该店还应交付的其它费用为每月10000元.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com