
某省两相近重要城市之间人员交流频繁,为了缓解交通压力,特修一条专用铁路,用一列火车作为交通车,已知该车每次拖4节车厢,一日能来回16次, 如果每次拖7节车厢,则每日能来回10次.
(1)若每日来回的次数是车头每次拖挂车厢节数的一次函数,求此一次函数解析式:
(2)在(1)的条件下,每节车厢能载乘客110人.问这列火车每天来回多少次才能使运营人数最多?并求出每天最多运营人数。
科目:高中数学 来源: 题型:解答题
(文科题)(本小题12分)
要建造一个无盖长方体水池,底面一边长固定为8m,最大装水量为72m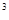 ,池底和池壁的造价分别为2
,池底和池壁的造价分别为2 元/
元/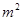 、
、 元/
元/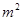 ,怎样设计水池底的另一边长和水池的高,才能使水池的总造价最低?最低造价是多少?
,怎样设计水池底的另一边长和水池的高,才能使水池的总造价最低?最低造价是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(14分)病人按规定的剂量服用某药物,测得服药后,每毫升血液中含药量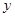 (毫克)与时间
(毫克)与时间 (小时)满足:前1小时内成正比例递增,1小时后按指数型函数
(小时)满足:前1小时内成正比例递增,1小时后按指数型函数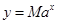 (
(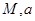 为常数)衰减.如图是病人按规定的剂量服用该药物后,每毫升血液中药物含量随时间变化的曲线.
为常数)衰减.如图是病人按规定的剂量服用该药物后,每毫升血液中药物含量随时间变化的曲线.
(1)求函数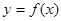 的解析式;
的解析式;
(2)已知每毫升血液中含药量不低于0.5毫克时有治疗效果,低于0.5毫克时无治疗效果.求病人一次服药后的有效治疗时间为多少小时?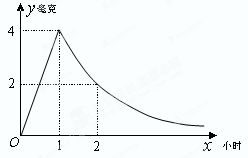
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)已知y= 是二次函数,且f(0)=8及f(x+1)-f(x)=-2x+1
是二次函数,且f(0)=8及f(x+1)-f(x)=-2x+1
(1)求 的解析式;
的解析式;
(2)求函数 的单调递减区间及值域..
的单调递减区间及值域..
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知f(x)=logax,g(x)=2loga(2x+t-2)(a>0,a≠1,t∈R).
(1)当t=4,x∈[1,2],且F(x)=g(x)-f(x)有最小值2时,求a的值;
(2)当0<a<1,x∈[1,2]时,有f(x)≥g(x)恒成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本大题13分)设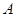 、
、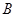 为函数
为函数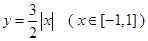 图象上不同的两个点,
图象上不同的两个点,
且 AB∥ 轴,又有定点
轴,又有定点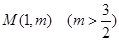 ,已知
,已知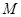 是线段
是线段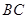 的中点.
的中点.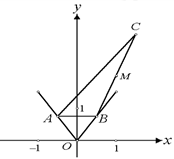
⑴ 设点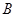 的横坐标为
的横坐标为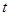 ,写出
,写出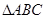 的面积
的面积 关于
关于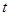 的函数
的函数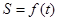 的表达式;
的表达式;
⑵ 求函数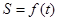 的最大值,并求此时点
的最大值,并求此时点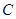 的坐标。
的坐标。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com