
设底部为等边三角形的直棱柱的体积为V,那么其表面积最小时,底面边长为( )
A.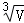 B.
B.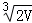 C.
C.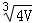 D.
D.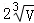
科目:高中数学 来源:[同步]2014年湘教版必修二 3.1 弧度制与任意角练习卷1(解析版) 题型:解答题
在单位圆中画出适合下列条件的角α的终边的范围,并由此写出角α的集合:

(1)sin α≥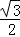 ;
;
(2)cos α≤﹣ .
.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版必修三 7.1 解析几何初步练习卷(解析版) 题型:解答题
在△ABC中,已知点A(5,﹣2)、B(7,3),且边AC的中点M在y轴上,边BC的中点N在x轴上.
(1)求点C的坐标;
(2)求直线MN的方程.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教B版选修4-5 2.3平均值不等式练习卷(解析版) 题型:填空题
(2014•湖北)设f(x)是定义在(0,+∞)上的函数,且f(x)>0,对任意a>0,b>0,若经过点(a,f(a)),(b,﹣f(b))的直线与x轴的交点为(c,0),则称c为关于函数f(x)的平均数,记为Mf(a,b),例如,当f(x)=1(x>0)时,可得Mf(a,b)=c=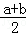 ,即Mf(a,b)为a,b的算术平均数.
,即Mf(a,b)为a,b的算术平均数.
(1)当f(x)= (x>0)时,Mf(a,b)为a,b的几何平均数;
(2)当f(x)= (x>0)时,Mf(a,b)为a,b的调和平均数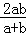 ;
;
(以上两空各只需写出一个符合要求的函数即可)
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教B版选修4-5 2.3平均值不等式练习卷(解析版) 题型:选择题
已知a,b,c是正实数,且ab+bc+ac=1,则abc的最大值为( )
A.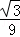 B.
B.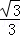 C.1 D.
C.1 D.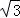
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教B版选修4-5 2.3平均值不等式练习卷(解析版) 题型:选择题
(2007•北京)如果正数a,b,c,d满足a+b=cd=4,那么( )
A.ab≤c+d且等号成立时a,b,c,d的取值唯一
B.ab≥c+d且等号成立时a,b,c,d的取值唯一
C.ab≤c+d且等号成立时a,b,c,d的取值不唯一
D.ab≥c+d且等号成立时a,b,c,d的取值不唯一
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教B版选修4-5 2.2排序不等式练习卷(解析版) 题型:解答题
若a1≤a2≤…≤an,而b1≥b2≥…≥bn或a1≥a2≥…≥an而b1≤b2≤…≤bn,证明: ≤(
≤(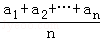 )•(
)•(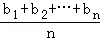 ).当且仅当a1=a2=…=an或b1=b2=…=bn时等号成立.
).当且仅当a1=a2=…=an或b1=b2=…=bn时等号成立.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教B版选修4-5 1.4绝对值的三角不等式练习卷(解析版) 题型:选择题
函数y=|x+1|+|2﹣x|的最小值是( )
A.3 B.2 C.1 D.0
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教B版选修4-5 1.2基本不等式练习卷(解析版) 题型:选择题
(2014•湖南模拟)设点G是△ABC的重心,若∠A=120°,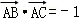 ,则
,则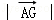 的最小值是( )
的最小值是( )
A.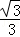 B.
B.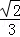 C.
C.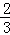 D.
D.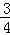
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com