
分析 (1)由向量垂直,$\overrightarrow{a}$•$\overrightarrow{b}$=(sinθ,-2)•(1,cosθ)=sinθ-2cosθ=0,tanθ=2,由正切函数的二倍角公式即可求得tan2θ的值;
(2)由$-\frac{π}{2}<θ-φ<\frac{π}{2}$,cos(θ-φ)=$\sqrt{1-si{n}^{2}(θ-φ)}$=$\frac{3\sqrt{10}}{10}$,由cosφ=cos[θ-(θ-φ)],根据两角差的余弦公式即可求得cosφ的值.
解答 解:(1)由$\overrightarrow{a}$⊥$\overrightarrow{b}$,
∴$\overrightarrow{a}$•$\overrightarrow{b}$=(sinθ,-2)•(1,cosθ)=sinθ-2cosθ=0,
∴tanθ=2,
∴$tan2θ=\frac{2tanθ}{{1-{{tan}^2}θ}}=-\frac{4}{3}$….(6分)
(2)∵$θ∈(0,\frac{π}{2})$,0<φ<$\frac{π}{2}$,
$-\frac{π}{2}<θ-φ<\frac{π}{2}$,
∴cos(θ-φ)>0,cos(θ-φ)=$\sqrt{1-si{n}^{2}(θ-φ)}$=$\frac{3\sqrt{10}}{10}$,
cosφ=cos[θ-(θ-φ)]=cosθcos(θ-φ)+sinθsin(θ-φ),
=$\frac{3\sqrt{10}}{10}$•$\frac{\sqrt{5}}{5}$+$\frac{\sqrt{10}}{10}$•$\frac{2\sqrt{5}}{5}$,
=$\frac{\sqrt{2}}{2}$.…(12分)
点评 本题考查向量数量积的坐标表示,考查向量垂直的充要条件,同角三角函数的基本关系,两角差的余弦公式,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | -1 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,0,1} | B. | {0,1} | C. | {0} | D. | {1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2Sn=an+1 | B. | Sn=2an+1 | C. | 2Sn=an-1 | D. | Sn=2an-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
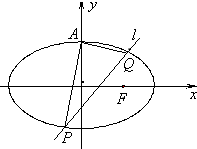 如图,已知椭圆$C:\frac{x^2}{a^2}+{y^2}=1(a>1)$的上顶点为A,右焦点为F,直线AF与圆M:x2+y2-6x-2y+7=0相切.
如图,已知椭圆$C:\frac{x^2}{a^2}+{y^2}=1(a>1)$的上顶点为A,右焦点为F,直线AF与圆M:x2+y2-6x-2y+7=0相切.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com