
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源:2016-2017学年安徽省六安市高一上学期周末作业(十三)数学试卷(解析版) 题型:选择题
已知棱长为1的正方体 中,
中,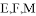 分别是
分别是 的中点,又
的中点,又 分别在线段
分别在线段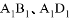 上,且
上,且 ,设面
,设面 面
面 ,则下列结论中不成立的是( )
,则下列结论中不成立的是( )

A.  面
面
B. 
C. 面 与面
与面 不垂直
不垂直
D. 当 变化时,
变化时, 不是定直线
不是定直线
查看答案和解析>>
科目:高中数学 来源:2017届河北省石家庄市高三第二次质量检测数学(理)试卷(解析版) 题型:填空题
非零向量 的夹角为
的夹角为 ,且满足
,且满足 ,向量组
,向量组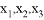 由一个
由一个 和两个
和两个 排列而成,向量组
排列而成,向量组 由两个
由两个 和一个
和一个 排列而成,若
排列而成,若 所有可能值中的最小值为
所有可能值中的最小值为 ,则
,则 __________.
__________.
查看答案和解析>>
科目:高中数学 来源:2017届河北省石家庄市高三第二次质量检测数学(理)试卷(解析版) 题型:选择题
若 ,则在
,则在 的展开式中,
的展开式中,  的幂函数不是整数的项共有( )
的幂函数不是整数的项共有( )
A. 13项 B. 14项 C. 15项 D. 16项
查看答案和解析>>
科目:高中数学 来源:2017届贵州省贵阳市高三2月适应性考试(一)数学理试卷(解析版) 题型:解答题
选修4-4:坐标系与参数方程
在直角坐标系中,以坐标原点为极点, 
轴的正半轴为极轴建立极坐标系,曲线
的极坐标方程为
,直线
的参数方程为
(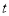
为参数).
(1)求曲线
的普通方程;
(2)若直线
与曲线
交于
两点,点
的坐标为
,求
的值.
查看答案和解析>>
科目:高中数学 来源:2017届贵州省贵阳市高三2月适应性考试(一)数学理试卷(解析版) 题型:填空题
我国古代数学家刘徽是公元三世纪世界上最杰出的数学家,他在《九章算术圆田术》注中,用割圆术证明了圆面积的精确公式,并给出了计算圆周率的科学方法.所谓“割圆术”,即通过圆内接正多边形细割圆,并使正多边形的周长无限接近圆的周长,进而来求得较为精确的圆周率(圆周率指圆周长与该圆直径的比率).刘徽计算圆周率是从正六边形开始的,易知圆的内接正六边形可分为六个全等的正三角形,每个三角形的边长均为圆的半径
,此时圆内接正六边形的周长为
,此时若将圆内接正六边形的周长等同于圆的周长,可得圆周率为3,当用正二十四边形内接于圆时,按照上述算法,可得圆周率为__________.(参考数据: 
)
查看答案和解析>>
科目:高中数学 来源:2017届河北省高三下学期二调考试数学(理)试卷(解析版) 题型:解答题
设 ,曲线
,曲线 在点
在点 处的切线与直线
处的切线与直线 垂直.
垂直.
(1)求 的值;
的值;
(2)若对于任意的 ,
,  恒成立,求
恒成立,求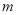 的取值范围;
的取值范围;
(3)求证:  .
.
查看答案和解析>>
科目:高中数学 来源:2017届甘肃省兰州市高三第一次诊断性考试数学(文) 试卷(解析版) 题型:选择题
已知等差数列 的前
的前 项和为
项和为 ,若
,若 ,
, ,则
,则 ( )
( )
A. 45 B. 90 C. 120 D. 75
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com