
分析 (1)利用cos2α+sin2α=1可把曲线C的参数方程$\left\{\begin{array}{l}{x=2cosα}\\{y=\sqrt{5}sinα}\end{array}\right.$(α为参数)化为直角坐标方程,直线l的极坐标轴方程为ρcos(θ-$\frac{π}{4}$)=2$\sqrt{2}$,展开$\frac{\sqrt{2}}{2}(ρcosθ+ρsinθ)=2\sqrt{2}$,利用$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$即可化为直角坐标方程.
(2)设点P的坐标为$(2cosα,\sqrt{5}sinα)$,利用点到直线的距离公式可得P到直线l的距离d=$\frac{|2cosα+\sqrt{5}sinα-4|}{\sqrt{2}}$,再利用三角函数的单调性即可得出.
解答 解:(1)曲线C的参数方程为$\left\{\begin{array}{l}{x=2cosα}\\{y=\sqrt{5}sinα}\end{array}\right.$(α为参数),曲线C的直角坐标方程:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{5}$=1,
直线l的极坐标轴方程为ρcos(θ-$\frac{π}{4}$)=2$\sqrt{2}$,展开$\frac{\sqrt{2}}{2}(ρcosθ+ρsinθ)=2\sqrt{2}$,ρcosθ+ρsinθ=4,
∴直线l的直角坐标方程为x+y=4.
(2)设点P的坐标为$(2cosα,\sqrt{5}sinα)$,
得P到直线l的距离d=$\frac{|2cosα+\sqrt{5}sinα-4|}{\sqrt{2}}$,令sinφ=$\frac{2}{3}$,cosφ=$\frac{\sqrt{5}}{3}$.
则d=$\frac{|3sin(α+φ)-4|}{\sqrt{2}}$,显然当sin(α+φ)=-1时,dmax=$\frac{7\sqrt{2}}{2}$.此时α+φ=2kπ+$\frac{3π}{2}$,k∈Z.
∴cosα=$cos(2kπ+\frac{3π}{2}-φ)$=-sinφ=-$\frac{2}{3}$.sinα=sin$(2kπ+\frac{3π}{2}-φ)$=-cosφ=-$\frac{\sqrt{5}}{3}$,即P$(-\frac{4}{3},-\frac{5}{3})$.
点评 本题考查了把参数方程化为普通方程、极坐标方程化为直角坐标方程、点到直线的距离公式、三角函数的单调性,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{4}{9}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\sqrt{17}$ | C. | $\frac{3\sqrt{2}}{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=x${\;}^{\frac{1}{2}}$ | B. | f(x)=x3 | C. | f(x)=($\frac{1}{2}$)x | D. | f(x)=3x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
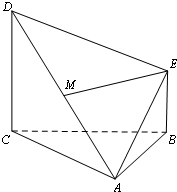 如图,多面体ABCDE中,CD⊥平面ABC,BE⊥平面ABC,AB=BC,BE=$\frac{1}{2}$CD,
如图,多面体ABCDE中,CD⊥平面ABC,BE⊥平面ABC,AB=BC,BE=$\frac{1}{2}$CD,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com