
(本小题满分10分)如图,在直三棱柱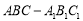 中,已知
中,已知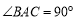 ,
,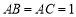 ,
,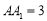 ,点
,点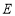 ,
,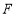 分别在棱
分别在棱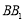 ,
,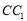 上,且
上,且 ,
,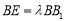 ,
,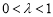 .
.
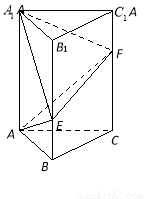
(1)当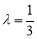 时,求异面直线
时,求异面直线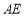 与
与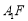 所成角的大小;
所成角的大小;
(2)当直线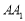 与平面
与平面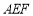 所成角的正弦值为
所成角的正弦值为 时,求
时,求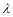 的值.
的值.
(1) (2)
(2) .
.
【解析】
试题分析:(1)利用空间向量求异面直线所成角,关键明确各点坐标,利用空间向量数量积求夹角: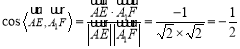 ,又异面直线
,又异面直线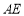 与
与 所成角不为钝角,所以异面直线
所成角不为钝角,所以异面直线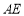 与
与 所成角为
所成角为 .(2)利用空间向量表示线面角,关键求出平面的法向量,再利用直线与平面所成角的正弦值等于直线与平面法向量所成角余弦值的绝对值求解. 平面
.(2)利用空间向量表示线面角,关键求出平面的法向量,再利用直线与平面所成角的正弦值等于直线与平面法向量所成角余弦值的绝对值求解. 平面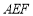 的法向量
的法向量 满足
满足 ,且
,且 .所以
.所以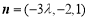 ,
,
 ,解得
,解得
试题解析:建立如图所示的空间直角坐标系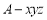 .
.
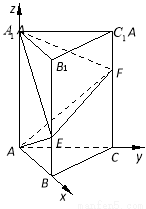
(1)因为AB=AC=1, 3,
3, ,
,
所以各点的坐标为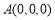 ,
, ,
, ,
,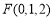 .
.
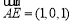 ,
, . 2分
. 2分
因为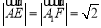 ,
,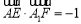 ,
,
所以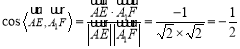 .所以向量
.所以向量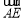 和
和 所成的角为
所成的角为 ,
,
所以异面直线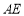 与
与 所成角为
所成角为 . 4分
. 4分
(2)因为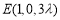 ,
,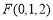 ,所以
,所以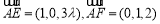 .
.
设平面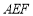 的法向量为
的法向量为 ,
,
则 ,且
,且 .
.
即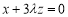 ,且
,且 .令
.令 ,则
,则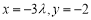 .
.
所以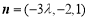 是平面
是平面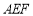 的一个法向量. 6分
的一个法向量. 6分
又 ,则
,则 ,
,
又因为直线 与平面
与平面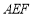 所成角的正弦值为
所成角的正弦值为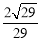 ,
,
所以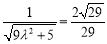 ,解得,
,解得, . 10分
. 10分
考点:利用空间向量求线线角、线面角


科目:高中数学 来源:2014-2015学年北京市东城区示范校高三上学期综合能力测试理科数学试卷(解析版) 题型:填空题
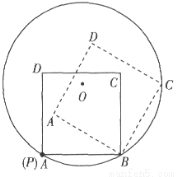
圆O的半径为1,P为圆周上一点,现将如图装置的边长为1的正方形(实线所示,正方形的顶点A与点P重合)沿圆周顺时针滚动,经过若干次滚动,点A第一次回到点P的位置,则点A走过的路径的长度为____________.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省泰安市高三上学期期末考试理科数学试卷(解析版) 题型:选择题
设函数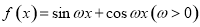 的最小正周期为
的最小正周期为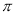 ,将
,将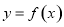 的图象向左平移
的图象向左平移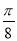 个单位得函数
个单位得函数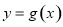 的图象,则
的图象,则
A. 上单调递减
上单调递减
B.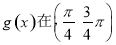 上单调递减
上单调递减
C. 上单调递增
上单调递增
D.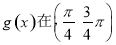 上单调递增
上单调递增
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省宿迁市高三上学期第一次摸底考试理科数学试卷(解析版) 题型:解答题
已知函数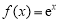 (其中
(其中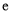 是自然对数的底数),
是自然对数的底数),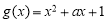 ,
,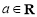 .
.
(1)记函数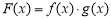 ,且
,且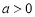 ,求
,求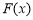 的单调增区间;
的单调增区间;
(2)若对任意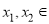
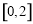 ,
,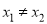 ,均有
,均有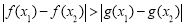 成立,求实数
成立,求实数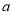 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河北唐山市高三上学期期末考试文科数学试卷(解析版) 题型:解答题
(本小题满分12分)如图,四棱锥 的底面ABCD是平行四边形,
的底面ABCD是平行四边形, 底面ABCD,
底面ABCD,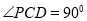 ,
,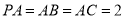 .
.

(1)求证: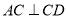 ;
;
(2)点E是棱PC的中点,求点B到平面EAD的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com