
对于四个正数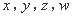 ,如果
,如果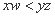 ,那么称
,那么称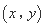 是
是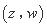 的“下位序对”.
的“下位序对”.
(1)对于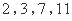 ,试求
,试求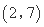 的“下位序对”;
的“下位序对”;
(2)设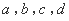 均为正数,且
均为正数,且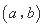 是
是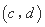 的“下位序对”,试判断
的“下位序对”,试判断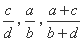 之间的大小关系;
之间的大小关系;
(3)设正整数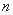 满足条件:对集合
满足条件:对集合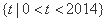 内的每个
内的每个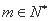 ,总存在
,总存在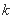
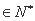 ,使得
,使得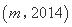 是
是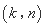 的“下位序对”,且
的“下位序对”,且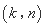 是
是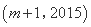 的“下位序对”.求正整数
的“下位序对”.求正整数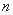 的最小值.
的最小值.
科目:高中数学 来源: 题型:
已知抛物线x2=4y,过原点作斜率为1的直线交抛物线于第一象限内一点P1,又过点P1作斜率为 的直线交抛物线于点P2,再过P2作斜率为
的直线交抛物线于点P2,再过P2作斜率为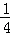 的直线交抛物线于点P3,﹣2<x<4,如此继续.一般地,过点3<x<5作斜率为
的直线交抛物线于点P3,﹣2<x<4,如此继续.一般地,过点3<x<5作斜率为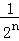 的直线交抛物线于点Pn+1,设点Pn(xn,yn).
的直线交抛物线于点Pn+1,设点Pn(xn,yn).
(1)求x3﹣x1的值;
(2)令bn=x2n+1﹣x2n﹣1,求证:数列{bn}是等比数列;
(3)记P奇(x奇,y奇)为点列P1,P3,…,P2n﹣1,…的极限点,求点P奇的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知A,B,C是 ABC的三个内角,
ABC的三个内角,
 (1)若
(1)若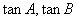 是方程
是方程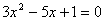 的两个实数根,判断
的两个实数根,判断 ABC的形状?
ABC的形状?
(2)若tanA+ tanB+ 1= tanA tanB ,求角C的大小
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com