
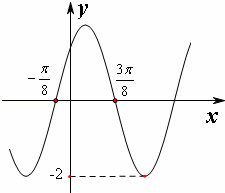
已知函数f(x)=Asin(ωx+ϕ),(A>0,ω>0,0≤ϕ≤π)的部分图象如图所示,则y=f(x)的解析式是f(x)= .
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
某体育用品商场经营一批每件进价为40元的运动服,先做了市场调查,得到数据如下表:
| 销售单价x(元) | 60 | 62 | 64 | 66 | 68 | … |
| 销售量y(件) | 600 | 580 | 560 | 540 | 520 | … |
根据表中数据,解答下列问题:
⑴ 建立一个恰当的函数模型,使它能较好地反映销售量y(件)与销售单价x(元)之间的函数关系,并写出这个函数模型的解析式 ;
;
⑵ 试求销售利润z(元)与销售单价x(元)之间的函数关系式(销售利润 = 总销售收入 - 总进价成本)并求价格为多少利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
对于四个正数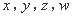 ,如果
,如果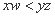 ,那么称
,那么称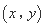 是
是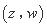 的“下位序对”.
的“下位序对”.
(1)对于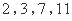 ,试求
,试求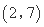 的“下位序对”;
的“下位序对”;
(2)设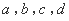 均为正数,且
均为正数,且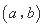 是
是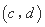 的“下位序对”,试判断
的“下位序对”,试判断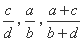 之间的大小关系;
之间的大小关系;
(3)设正整数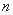 满足条件:对集合
满足条件:对集合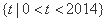 内的每个
内的每个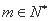 ,总存在
,总存在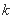
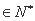 ,使得
,使得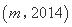 是
是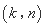 的“下位序对”,且
的“下位序对”,且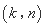 是
是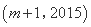 的“下位序对”.求正整数
的“下位序对”.求正整数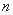 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com