练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知椭圆经过点，且离心率为.

    （1）求椭圆的方程；

    （2）若点、在椭圆上，且四边形是矩形，求矩形的面积的最大值.

    【答案】（1）（2）矩形面积的最大值为.

    【解析】

    （1）由椭圆过点，且离心率为，得到，，进而可求出结果；

    （2）先由题意知直线不垂直于轴，设直线，联立直线与椭圆方程，设，，根据韦达定理和题中条件可求出；再求出的最大值即可得出结果.

    解：（1）因为椭圆经过点，且离心率为，

    所以，，又因为，

    可解得，，焦距为.

    所求椭圆的方程为.

    （2）由题意知直线不垂直于轴，可设直线，

    由得，

    设，，则，

    又因为，，

    所以

    化简可得.

    所以

    设，，则，

    所以.

    令，因为

    所以在上单调递减，所以.

    设直线与轴交于点，

    因为矩形面积

    所以矩形面积的最大值为.

    此时直线.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的左顶点为，两个焦点与短轴一个顶点构成等腰直角三角形，过点且与x轴不重合的直线l与椭圆交于M，N不同的两点．

    （Ⅰ）求椭圆P的方程；

    （Ⅱ）当AM与MN垂直时，求AM的长；

    （Ⅲ）若过点P且平行于AM的直线交直线于点Q，求证：直线NQ恒过定点．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，，其中．

    讨论函数与的图象的交点个数；

    若函数与的图象无交点，设直线与的数和的图象分别交于点P，证明：．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的短轴长为，离心率为。

    （1）求椭圆的标准方程;

    （2）设椭圆的左，右焦点分别为，左，右顶点分别为，，点，，为椭圆上位于轴上方的两点，且，记直线，的斜率分别为，，若，求直线的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，动点到两坐标轴的距离之和等于它到定点的距离，记点P的轨迹为，给出下列四个结论：①关于原点对称；②关于直线对称；③直线与有无数个公共点；④在第一象限内，与x轴和y轴所围成的封闭图形的面积小于.其中正确的结论是________.（写出所有正确结论的序号）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司推出一新款手机，因其功能强大，外观新潮，一上市便受到消费者争相抢购，销量呈上升趋势.散点图是该款手机上市后前6周的销售数据.

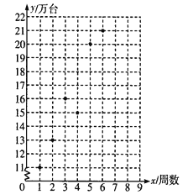
    （1）根据散点图，用最小二乘法求关于的线性回归方程，并预测该款手机第8周的销量；

    （2）为了分析市场趋势，该公司市场部从前6周的销售数据中随机抽取2周的数据，记抽取的销量在18万台以上的周数为，求的分布列和数学期望.参考公式：回归直线方程，其中：，.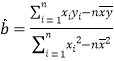

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的焦距为分别为椭圆的左、右顶点，为椭圆上的两点(异于)，连结，且斜率是斜率的倍.

    （1）求椭圆的方程；

    （2）证明:直线恒过定点.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （Ⅰ）在图中作出函数y =的图象，并求出其与直线围成的封闭图形的面积；

    （Ⅱ）若g(x)=|2x-a|+|x-1|.当+g(x)≥3对一切实数x恒成立，求实数a的范围。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数()，曲线在点处的切线方程为.

    (1)求实数的值，并求的单调区间；

    (2)试比较与的大小，并说明理由；

    (3)求证：

    查看答案和解析>>

    同步练习册答案