Question

一只青蛙从数轴的原点出发，当投下的硬币正面向上时，它沿数轴的正方向跳动两个单位；当投下的硬币反面向上时，它沿数轴的负方向跳动一个单位．若青蛙跳动4次停止，设停止时青蛙在数轴上对应的坐标为X，则E（X）=    ．

Answer 1

【答案】分析：列举出所有的可能出现的情况，硬币4次都反面向上，则青蛙停止时坐标为x₁=-4，硬币3次反面向上而1次正面向上，硬币2次反面向上而2次正面向上，硬币1次反面向上而3次正面向上，硬币4次都正面向上，做出对应的坐标和概率，算出期望．
解答：解：所有可能出现的情况分别为
硬币4次都反面向上，则青蛙停止时坐标为x₁=-4，此时概率；
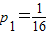
硬币3次反面向上而1次正面向上，则青蛙停止时坐标为x₂=-1，此时概率；
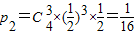
硬币2次反面向上而2次正面向上，则青蛙停止时坐标为x₃=2，此时概率；
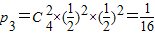
硬币1次反面向上而3次正面向上，则青蛙停止时坐标为x₄=5，此时概率；
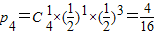
硬币4次都正面向上，则青蛙停止时坐标为x₅=8，此时概率，
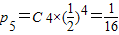
∴E（X）=x₁p₁+x₂p₂+x₃p₃+x₄p₄+x₅p₅=2．
故答案为：2
点评：本题考查离散型随机变量的分布列和期望，这是近几年经常出现的一个问题，可以作为解答题出现，考查的内容通常是以分布列和期望为载体，进而考查其他的知识点．
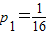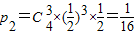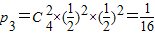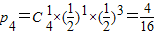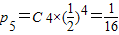