
分析 (Ⅰ)依题意求得K的坐标与直线l的方程.设P(x,y),可知T'(x,-1),T(x,2y+1).把T的坐标代入圆C的方程,可得动点P的轨迹Γ的方程;
(Ⅱ)依题意,不妨设A(-2,0),B(2,0),设OM的斜率为k1,可得AP的斜率也为k1;同理,设OM的斜率为k2,可得BP的斜率也为k2.写出AP、BP方程,分别与椭圆方程联立,整理可得${k_1}•{k_2}=-\frac{1}{4}$,不妨设k1>0,k2<0.再写出OM,ON的方程,与椭圆方程联立,求出M,N的坐标,求得|OM|,再由点到直线的距离公式求出N到OM的距离d.代入三角形OMN的面积整理得答案.
解答 解:(Ⅰ)依题意,可知K(0,-1),直线l:x=-1.
设P(x,y),依题意,可知T'(x,-1),T(x,2y+1).
∵T为C:x2+(y-1)2=4上动点,∴C:x2+(2y+1-1)2=4,
可得动点P的轨迹Γ的方程$\frac{x^2}{4}+{y^2}=1$;
(Ⅱ)依题意,不妨记A(-2,0),B(2,0),设OM的斜率为k1,
∵OM∥AP,∴AP的斜率也为k1;
同理,设OM的斜率为k2,
∵ON∥BP,∴BP的斜率也为k2.
设P(x0,y0),由$\left\{{\begin{array}{l}{y={k_1}(x+2)}\\{{x^2}+4{y^2}=4}\end{array}}\right.$,得$(1+4{{k}_{1}}^{2}){x}^{2}+16{{k}_{1}}^{2}x+16{{k}_{1}}^{2}-4=0$,
则${x}_{0}-2=\frac{-16{{k}_{1}}^{2}}{1+4{{k}_{1}}^{2}}$ ①;
同理,由$\left\{{\begin{array}{l}{y={k_2}(x-2)}\\{{x^2}+4{y^2}=4}\end{array}}\right.$,得$(1+4{{k}_{2}}^{2}){x}^{2}-16{{k}_{2}}^{2}x+16{{k}_{2}}^{2}-4=0$,
则${x}_{0}+2=\frac{16{{k}_{2}}^{2}}{1+4{{k}_{2}}^{2}}$ ②.
联立①②,消去x0可得${k_1}•{k_2}=-\frac{1}{4}$,不妨设k1>0,k2<0.
由$\left\{\begin{array}{l}{y={k}_{1}x}\\{{x}^{2}+4{y}^{2}=4}\end{array}\right.$,可得M($\frac{2}{\sqrt{1+4{{k}_{1}}^{2}}}$,$\frac{2{k}_{1}}{\sqrt{1+4{{k}_{1}}^{2}}}$),则|OM|=$\sqrt{\frac{4(1+{{k}_{1}}^{2})}{1+4{{k}_{1}}^{2}}}$.
由$\left\{\begin{array}{l}{y={k}_{2}x}\\{{x}^{2}+4{y}^{2}=4}\end{array}\right.$,可得N($-\frac{2}{\sqrt{1+4{{k}_{1}}^{2}}}$,$\frac{2{k}_{2}}{\sqrt{1+4{{k}_{1}}^{2}}}$).
则N到OM的距离d=$\sqrt{\frac{4({k}_{1}-{k}_{2})^{2}}{(1+4{{k}_{2}}^{2})(1+{{k}_{1}}^{2})}}$.
则三角形OMN的面积$S=\frac{1}{2}|{OM}|•d$=$\frac{1}{2}\sqrt{\frac{4(1+{{k}_{1}}^{2})}{1+4{{k}_{1}}^{2}}}•\sqrt{\frac{4({k}_{1}-{k}_{2})^{2}}{(1+4{{k}_{2}}^{2})(1+{{k}_{1}}^{2})}}$=$\sqrt{\frac{({k}_{1}-{k}_{2})^{2}}{{{k}_{1}}^{2}+{{k}_{2}}^{2}+\frac{1}{2}}}$
=$\sqrt{\frac{({k}_{1}-{k}_{2})^{2}}{{{k}_{1}}^{2}+{{k}_{2}}^{2}-2{k}_{1}•{k}_{2}}}=1$.
点评 本题考查椭圆的简单性质,考查了直线与椭圆位置关系的应用,考查计算能力,体现了“设而不求”的解题思想方法,是中档题.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{16}$ | B. | 7 | C. | 16 | D. | 28 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
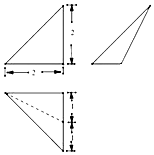
| A. | $2\sqrt{5}$ | B. | $2\sqrt{3}$ | C. | $2\sqrt{2}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | ±1 | C. | -1 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 平均车速超过100km/h人数 | 平均车速不超过100km/h人数 | 合计 | |
| 男性驾驶员人数 | |||
| 女性驾驶员人数 | |||
| 合计 | |||
| P(K2≥k0) | 0.150 | 0.100 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
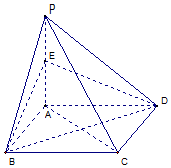 如图,点P为矩形ABCD所在平面外一点,PA⊥平面ABCD,点E为PA的中点.
如图,点P为矩形ABCD所在平面外一点,PA⊥平面ABCD,点E为PA的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com