
【题目】已知函数![]() .
.
(1)求![]() 在区间
在区间![]() 上的最大值;
上的最大值;
(2)若过点![]() 存在3条直线与曲线
存在3条直线与曲线![]() 相切,求t的取值范围;
相切,求t的取值范围;
(3)问过点![]() 分别存在几条直线与曲线
分别存在几条直线与曲线![]() 相切?(只需写出结论)
相切?(只需写出结论)
【答案】
【解析】试题分析:(1)求导数,导数等于0求出![]() ,再代入原函数解析式,最后比较大小,即可;(2)设切点,由相切得出切线方程,然后列表并讨论求出结果;(3)由(2)容易得出结果.
,再代入原函数解析式,最后比较大小,即可;(2)设切点,由相切得出切线方程,然后列表并讨论求出结果;(3)由(2)容易得出结果.
(1)由![]() 得
得![]() ,令
,令![]() ,得
,得![]() 或
或![]() ,
,
因为![]() ,
, 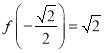 ,
, 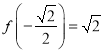 ,
, ![]() ,
,
所以![]() 在区间
在区间![]() 上的最大值为
上的最大值为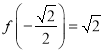 .
.
(2)设过点P(1,t)的直线与曲线![]() 相切于点
相切于点![]() ,则
,则
![]() ,且切线斜率为
,且切线斜率为![]() ,所以切线方程为
,所以切线方程为![]() ,
,
因此![]() ,整理得:
,整理得: ![]() ,
,
设![]()
![]() ,则“过点
,则“过点![]() 存在3条直线与曲线
存在3条直线与曲线![]() 相切”等价于“
相切”等价于“![]() 有3个不同零点”,
有3个不同零点”, ![]()
![]() =
=![]() ,
,
![]() 与
与![]() 的情况如下:
的情况如下:
|
| 0 |
| 1 |
|
| + | 0 |
| 0 | + |
|
| t+3 |
|
|
|
所以, ![]() 是
是![]() 的极大值,
的极大值, ![]() 是
是![]() 的极小值,
的极小值,
当![]() ,即
,即![]() 时,此时
时,此时![]() 在区间
在区间![]() 和
和![]() 上分别至多有1个零点,所以
上分别至多有1个零点,所以
![]() 至多有2个零点,
至多有2个零点,
当![]() ,
, ![]() 时,此时
时,此时![]() 在区间
在区间![]() 和
和![]() 上分别至多有1个零点,所以
上分别至多有1个零点,所以
![]() 至多有2个零点.
至多有2个零点.
当![]() 且
且![]() ,即
,即![]() 时,因为
时,因为![]() ,
,![]() ,
,
所以![]() 分别为区间
分别为区间![]() 和
和![]() 上恰有1个零点,由于
上恰有1个零点,由于![]() 在区间
在区间![]() 和
和![]() 上单调,所以
上单调,所以![]() 分别在区间
分别在区间![]() 和
和![]() 上恰有1个零点.
上恰有1个零点.
综上可知,当过点![]() 存在3条直线与曲线
存在3条直线与曲线![]() 相切时,t的取值范围是
相切时,t的取值范围是![]() .
.
(3)过点A(-1,2)存在3条直线与曲线![]() 相切;
相切;
过点B(2,10)存在2条直线与曲线![]() 相切;
相切;
过点C(0,2)存在1条直线与曲线![]() 相切.
相切.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sinωx+![]() cosωx的最小正周期为π,x∈R,ω>0是常数.
cosωx的最小正周期为π,x∈R,ω>0是常数.
(1)求ω的值;
(2)若f(![]() +
+![]() )=
)=![]() , θ∈(0,
, θ∈(0,![]() ),求sin2θ.
),求sin2θ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)在R上可导,其导函数为f′(x),且函数y=(1﹣x)f′(x)的图象如图所示,则下列结论中一定成立的是( )
A.函数f(x)有极大值f(2)和极小值f(1)
B.函数f(x)有极大值f(﹣2)和极小值f(1)
C.函数f(x)有极大值f(2)和极小值f(﹣2)
D.函数f(x)有极大值f(﹣2)和极小值f(2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ax2﹣a﹣lnx,g(x)= ![]() ,其中a∈R,e=2.718…为自然对数的底数.
,其中a∈R,e=2.718…为自然对数的底数.
(1)讨论f(x)的单调性;
(2)证明:当x>1时,g(x)>0;
(3)确定a的所有可能取值,使得f(x)>g(x)在区间(1,+∞)内恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若在曲线![]() (或y=f(x))上两个不同点处的切线重合,则称这条切线为曲线f(x,y)=0或y=f(x)的“自公切线”。
(或y=f(x))上两个不同点处的切线重合,则称这条切线为曲线f(x,y)=0或y=f(x)的“自公切线”。
下列方程:
①![]() ;
;
②![]() ;
;
③y=3sinx+4cosx;
④![]()
对应的曲线中存在“自公切线”的有( )
A.①③
B.①④
C.②③
D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知图甲中的图象对应的函数y=f(x),则图乙中的图象对应的函数在下列给出的四式中只可能是( )
A.y=f(|x|)
B.y=|f(x)|
C.y=f(﹣|x|)
D.y=﹣f(|x|)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 过点
过点![]() ,且圆心
,且圆心![]() 在直线
在直线![]() 上,过点
上,过点![]() 的直线交圆
的直线交圆![]() 于
于![]() 两点,过点
两点,过点![]() 分别做圆
分别做圆![]() 的切线,记为
的切线,记为![]() .
.
(Ⅰ)求圆![]() 的方程;
的方程;
(Ⅱ)求证:直线![]() 的交点都在同一条直线上,并求出这条直线的方程.
的交点都在同一条直线上,并求出这条直线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人.女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.
(1)根据以上数据建立一个2×2的列联表;
(2)根据所给的独立检验临界值表,你最多能有多少把握认为性别与休闲方式有关系?附:独立检验临界值表
P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com