
【题目】已知向量 ![]() =(
=( ![]() ,﹣1),
,﹣1), ![]() =(
=( ![]() ,
, ![]() ),若存在非零实数k,t使得
),若存在非零实数k,t使得 ![]() =
= ![]() +(t2﹣3)
+(t2﹣3) ![]() ,
, ![]() =﹣k
=﹣k ![]() +t
+t ![]() ,且
,且 ![]() ⊥
⊥ ![]() ,试求:
,试求: ![]() 的最小值.
的最小值.
【答案】解:∵ ![]() =(
=( ![]() ,﹣1),
,﹣1), ![]() =(
=( ![]() ,
, ![]() ), ∴|
), ∴| ![]() |=
|= ![]() =2,|
=2,| ![]() |=
|=  =1,且
=1,且 ![]()
![]() =
= ![]() ×
× ![]() +(﹣1)×
+(﹣1)× ![]() =0
=0
∵ ![]() =
= ![]() +(t2﹣3)
+(t2﹣3) ![]() ,
, ![]() =﹣k
=﹣k ![]() +t
+t ![]() ,且
,且 ![]() ⊥
⊥ ![]() ,
,
∴ ![]()
![]() =0,即(
=0,即( ![]() +(t2﹣3)
+(t2﹣3) ![]() )(﹣k
)(﹣k ![]() +t
+t ![]() )=0
)=0
展开并化简,得﹣k ![]() 2+(﹣kt2+3k+t)
2+(﹣kt2+3k+t) ![]()
![]() +t(t2﹣3)
+t(t2﹣3) ![]() 2=0
2=0
将| ![]() |=2、|
|=2、| ![]() |=1和
|=1和 ![]()
![]() =0代入上式,可得
=0代入上式,可得
﹣4k+t(t2﹣3)=0,整理得k= ![]() (t3﹣3t)
(t3﹣3t)
∴ ![]() =
=  =
= ![]() t2+t﹣
t2+t﹣ ![]() =
= ![]() (t+2)2﹣
(t+2)2﹣ ![]()
由此可得,当t=﹣2时, ![]() 的最小值等于﹣
的最小值等于﹣ ![]()
【解析】根据向量数量积的坐标公式和性质,分别求出| ![]() |=2,|
|=2,| ![]() |=1且
|=1且 ![]()
![]() =0,由此将
=0,由此将 ![]()
![]() =0化简整理得到k=
=0化简整理得到k= ![]() (t3﹣3t).将此代入
(t3﹣3t).将此代入 ![]() ,可得关于t的二次函数,根据二次函数的单调性即可得到
,可得关于t的二次函数,根据二次函数的单调性即可得到 ![]() 的最小值.
的最小值.


科目:高中数学 来源: 题型:
【题目】设b和c分别是先后抛掷一枚骰子得到的点数,用随机变量ξ表示方程x2+bx+c=0实根的个数(重根按一个计).
(1)求方程x2+bx+c=0有实根的概率;
(2)求ξ的分布列和数学期望;
(3)求在先后两次出现的点数中有5的条件下,方程x2+bx+c=0有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了检验学习情况,某培训机构于近期举办一场竞赛活动,分别从甲、乙两班各抽取10名学员的成绩进行统计分析,其成绩的茎叶图如图所示(单位:分),假设成绩不低于90分者命名为“优秀学员”.
(1)分别求甲、乙两班学员成绩的平均分(结果保留一位小数);
(2)从甲班4名优秀学员中抽取两人,从乙班2名80分以下的学员中抽取一人,求三人平均分不低于90分的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi , yi)(i=1,2,…,n),用最小二乘法建立的回归方程为 ![]() =0.85x﹣85.71,则下列结论中不正确的是( )
=0.85x﹣85.71,则下列结论中不正确的是( )
A.y与x具有正的线性相关关系
B.回归直线过样本点的中心( ![]() ,
, ![]() )
)
C.若该大学某女生身高增加1cm,则其体重约增加0.85kg
D.若该大学某女生身高为170cm,则可断定其体重必为58.79kg
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,我市某居民小区拟在边长为1百米的正方形地块ABCD上划出一个三角形地块APQ种植草坪,两个三角形地块PAB与QAD种植花卉,一个三角形地块CPQ设计成水景喷泉,四周铺设小路供居民平时休闲散步,点P在边BC上,点Q在边CD上,记∠PAB=a. 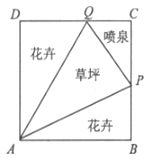
(1)当∠PAQ= ![]() 时,求花卉种植面积S关于a的函数表达式,并求S的最小值;
时,求花卉种植面积S关于a的函数表达式,并求S的最小值;
(2)考虑到小区道路的整体规划,要求PB+DQ=PQ,请探究∠PAQ是否为定值,若是,求出此定值,若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,圆![]() 的极坐标方程为
的极坐标方程为![]() ,若以极点
,若以极点![]() 为原点,极轴所在的直线为
为原点,极轴所在的直线为![]() 轴建立平面直角坐标系.
轴建立平面直角坐标系.
(1)求圆![]() 的参数方程;
的参数方程;
(2)在直线坐标系中,点![]() 是圆
是圆![]() 上的动点,试求
上的动点,试求![]() 的最大值,并求出此时点
的最大值,并求出此时点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com