分析:(I)利用三角形的中位线定理可证DE∥平面A1BC1.利用平行四边形的判定定理可证四边形ECC1A1是平行四边形,进而证明EC∥平面A1BC1,利用两个平面平行的判定定理得到平面DEC∥平面A1BC1.利用两个平面平行的性质定理可得结论;
(II)通过建立如图所示的空间直角坐标系,利用两个平面的法向量的夹角即可得出二面角.
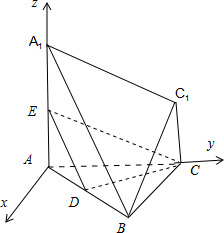
解答:证明:(I)在△AA
1B中,
∵D,E分别是AB,AA
1的中点,
∴DE∥BA
1,
又∵DE?平面A
1BC
1,A
1B?平面A
1BC
1,
∴DE∥平面A
1BC
1.
∵AA
1=2,CC
1=1,E分别是AA
1的中点,
∴EA
1=CC
1,
又∵CC
1∥AA
1,∴四边形ECC
1A
1是平行四边形,
∴EC∥A
1C
1.
而EC?平面A
1BC
1,A
1C
1?平面A
1BC
1,
∴EC∥平面A
1BC
1,
∵ED∩EC=E,ED,EC?平面DEC,
∴平面DEC∥平面A
1BC
1.
∴BC
1∥平面CDE;
(II)∵AA
1⊥平面ABC,
∴可以建立如图所示的空间直角坐标系,则E(0,0,1),A(0,0,0).
不妨设AC=4a(a>0),
∵AB⊥BC,AB=BC,D是AB的中点.
则C(0,4a,0),B(2a,2a,0),D(a,a,0).
∴
=(-a,3a,0),
=(-a,-a,1).
设平面CDE的法向量为
=(x,y,z),则
令y=1,则x=3,z=4a.
∴
=(3,1,4a).
∵AA
1⊥平面ABC,
∴可 取
=(0,0,2)作为平面ABC的法向量.
∴
cos<,>=
=
=
,
∴
sin<,>=
=
,
∴
tan<,>=
.
点评:熟练掌握三角形的中位线定理、平行四边形的判定和性质定理、线面与平面平行的判定和性质定理、通过建立如图所示的空间直角坐标系利用两个平面的法向量的夹角得出二面角是解题的关键.

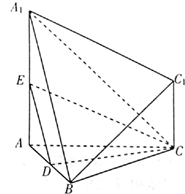 (2013•杭州二模)在几何体中,AA1⊥平面ABC,AB⊥BC,CC1∥AA1,AB=BC,AA1=2,CC1=1,D,E分别是AB,AA1的中点.
(2013•杭州二模)在几何体中,AA1⊥平面ABC,AB⊥BC,CC1∥AA1,AB=BC,AA1=2,CC1=1,D,E分别是AB,AA1的中点.

