
如下图,用A、B、C三类不同的元件连接两个系统N1,N2,当元件A、B、C都正常工作时系统N1正常工作,当元件A正常工作且元件B、C至少有一个正常工作时系统N2正常工作,已知元件A、B、C正常工作的概率分别为0.80,0.90,0.90,分别求系统N1,N2正常工作的概率p1,p2.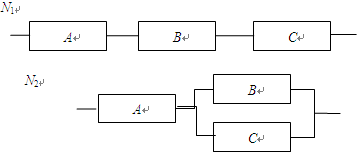
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:高中数学 来源: 题型:解答题
盒中装有5个产品,其中3个一等品,2个二等品,从中不放回地取产品,每次1个,求:
(1)取两次,两次都取得一等品的概率;
(2)取两次,第二次取得一等品的概率;
(3)取三次,第三次才取得一等品的概率;
(4)取两次,已知第二次取得一等品,求第一次取得是二等品的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校高三年级组为了缓解学生的学习压力,举办元宵猜灯谜活动。规定每人最多猜3道,在A区猜对一道灯谜获3元奖品;在B区猜对一道灯谜获2元奖品,如果前两次猜题后所获奖品总额超过3元即停止猜题,否则猜第三道题。假设某同学猜对A区的任意一道灯谜的概率为0.25,猜对B区的任意一道灯谜的概率为0.8,用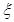 表示该同学猜灯谜结束后所得奖品的总金额。
表示该同学猜灯谜结束后所得奖品的总金额。
(1)若该同学选择先在A区猜一题,以后都在B区猜题,求随机变量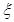 的数学期望
的数学期望 ;
;
(2)试比较该同学选择都在B区猜题所获奖品总额超过3元与选择(1)中方式所获奖品总额超过3元的概率的大小。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
袋子里有大小相同但标有不同号码的3个红球和4个黑球,从袋子里随机取出4个球.
⑴求取出的红球数?的概率分布列;
⑵若取到每个红球得2分,取到每个黑球得1分,求得分不超过5分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)一厂家向用户提供的一箱产品共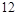 件,其中有
件,其中有 件次品,用户先对产品进行抽检以决定是否接收.抽检规则是这样的:一次取一件产品检查(取出的产品不放回箱子),若前三次没有抽查到次品,则用户接收这箱产品;若前三次中一抽查到次品就立即停止抽检,并且用户拒绝接收这箱产品.
件次品,用户先对产品进行抽检以决定是否接收.抽检规则是这样的:一次取一件产品检查(取出的产品不放回箱子),若前三次没有抽查到次品,则用户接收这箱产品;若前三次中一抽查到次品就立即停止抽检,并且用户拒绝接收这箱产品.
(Ⅰ)求这箱产品被用户接收的概率;
(Ⅱ)记抽检的产品件数为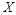 ,求随机变量
,求随机变量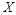 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
甲打靶射击,有4发子弹,其中有一发是空弹(“空弹”即只有弹体没有弹头的子弹).
(1)如果甲只射击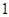 次,求在这一枪出现空弹的概率;
次,求在这一枪出现空弹的概率;
(2)如果甲共射击 次,求在这三枪中出现空弹的概率;
次,求在这三枪中出现空弹的概率;
(3)如果在靶上画一个边长为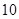 的等边
的等边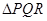 ,甲射手用实弹瞄准了三角形
,甲射手用实弹瞄准了三角形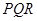 区域随机射击,且弹孔都落在三角形
区域随机射击,且弹孔都落在三角形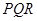 内。求弹孔与
内。求弹孔与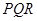 三个顶点的距离都大于1的概率(忽略弹孔大小).
三个顶点的距离都大于1的概率(忽略弹孔大小).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)甲、乙等五名环保志愿者被随机地分到 四个不同的岗位服务,每个岗位至少有一名志愿者.
四个不同的岗位服务,每个岗位至少有一名志愿者.
(1)求甲、乙两人同时参加 岗位服务的概率;
岗位服务的概率;
(2)求甲、乙两人不在同一个岗位服务的概率;
(3)设随机变量 为这五名志愿者中参加
为这五名志愿者中参加 岗位服务的人数,求
岗位服务的人数,求 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
朵朵小朋友用红、黄、蓝三种颜色的彩笔给下列三个图形随机涂色,每个图形只涂一种颜色,求:


(Ⅰ)三个图形颜色不全相同的概率;
(Ⅱ)三个图形颜色恰有两个相同的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)袋中装着标有数字1,2,3,4,5的小球各2个,从袋中任取3个小球,按3个小球上最大数字的9倍计分,每个小球被取出的可能性都相等,用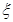 表示取出的3个小球上的最大数字,求:
表示取出的3个小球上的最大数字,求:
(Ⅰ)取出的3个小球上的数字互不相同的概率;
(Ⅱ)随机变量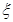 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)计分介于20分到40分之间的概率
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com