【答案】
分析:(I)函数f(x)的定义域为(0,+∞),求导函数,令f′(x)>0,分类讨论可得函数的单调区间;
(Ⅱ)(i)构造函数F(x)=f(1+x)+f(1-x)=2ln(1+x)+2ln(1-x)+2x
2,求导函数,确定F(x)在(0,1)上为减函数,从而可求实数m的取值范围;
(ii)由f(x
1)+f(x
2)=0,可得(x
1+x
2)
2=2x
1x
2-2lnx
1x
2+2设t=x
1x
2,则t>0,g(t)=2t-2lnt+2,求出g(t)
min,即可证得结论.
解答:(I)解:函数f(x)的定义域为(0,+∞),f′(x)=
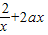
令f′(x)>0,∵x>0,∴2ax
2+2>0
①当a≥0时,f′(x)>0在(0,+∞)上恒成立,∴f(x)递增区间是(0,+∞);
②当a<0时,由2ax
2+2>0可得
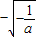
<x<
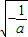
x>0,∴f(x)递增区间是(0,
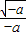
),递减区间为
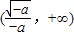
;
(Ⅱ)(i)解:设F(x)=f(1+x)+f(1-x)=2ln(1+x)+2ln(1-x)+2x
2,则F′(x)=
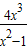
∵0<x<l,∴F′(x)<0在(0,1)上恒成立,∴F(x)在(0,1)上为减函数
∴F(x)<F(0)=0,∴m≥0,∴实数m的取值范围为[0,+∞);
(ii)证明:∵f(x
1)+f(x
2)=0,
∴21nx
1+x
12-1+21nx
2+x
22-1=0
∴2lnx
1x
2+(x
1+x
2)
2-2x
1x
2-2=0
∴(x
1+x
2)
2=2x
1x
2-2lnx
1x
2+2
设t=x
1x
2,则t>0,g(t)=2t-2lnt+2,∴g′(t)=
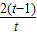
令g′(t)>0,得t>1,∴g(t)在(0,1)上单调递减,在(1,+∞)上单调递增
∴g(t)
min=g(1)=4,∴(x
1+x
2)
2>4,∴x
1+x
2>2.
点评:本题考查导数知识的运用,考查函数的单调性,考查函数的最值,解题的关键是构造函数,正确运用导数.

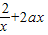
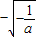 <x<
<x<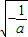
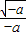 ),递减区间为
),递减区间为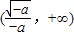 ;
;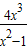
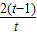


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案