
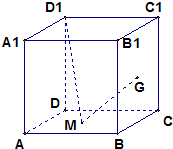
 已知正方体的棱长ABCD-A1B1C1D1的棱长为2,G是面BB1C1C的中心,M为面ABCD上一点,则D1M+GM的最小值为
已知正方体的棱长ABCD-A1B1C1D1的棱长为2,G是面BB1C1C的中心,M为面ABCD上一点,则D1M+GM的最小值为 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:
 8、如图,已知正方体ABCD-A1B1C1D1的棱长为3,点E,F在线段AB上,点M在线段B1C1上,点N在线段C1D1上,且EF=1,D1N=x,AE=y,M是B1C1的中点,则四面体MNEF的体积( )
8、如图,已知正方体ABCD-A1B1C1D1的棱长为3,点E,F在线段AB上,点M在线段B1C1上,点N在线段C1D1上,且EF=1,D1N=x,AE=y,M是B1C1的中点,则四面体MNEF的体积( )查看答案和解析>>
科目:高中数学 来源:黄冈中学 高二数学(下册)、考试卷5 简单几何体同步测试卷(二) 题型:013
已知正方体![]() 的棱长为1,点M在棱AB上,且
的棱长为1,点M在棱AB上,且![]() ,点P是平面ABCD内的动点,且点P到直线
,点P是平面ABCD内的动点,且点P到直线![]() 的距离与点P到点M的距离的平方差为1,则点P的轨迹为
的距离与点P到点M的距离的平方差为1,则点P的轨迹为
A.抛物线
B.双曲线
C.直线
D.以上都不对
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
已知正方体 的棱长为2,分别按下列要求建立空间直角坐标系,请写出正方体各顶点的坐标.
的棱长为2,分别按下列要求建立空间直角坐标系,请写出正方体各顶点的坐标.
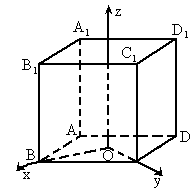
(1)如图,以底面ABCD的中心O为坐标原点,分别以射线AB、BC、 的指向为Ox轴、Oy轴、Oz轴的正方向,建立直角坐标系;
的指向为Ox轴、Oy轴、Oz轴的正方向,建立直角坐标系;

(2)如图,以底面正方形ABCD的中心为坐标原点O,分别以射线OB、OC、 的指向为Ox轴、Oy轴、Oz轴的正方向,建立直角坐标系.
的指向为Ox轴、Oy轴、Oz轴的正方向,建立直角坐标系.

查看答案和解析>>
科目:高中数学 来源: 题型:044
已知正方体
 的棱长为2,分别按下列要求建立空间直角坐标系,请写出正方体各顶点的坐标.
的棱长为2,分别按下列要求建立空间直角坐标系,请写出正方体各顶点的坐标.
(1)
如图,以底面ABCD的中心O为坐标原点,分别以射线AB、BC、 的指向为Ox轴、Oy轴、Oz轴的正方向,建立直角坐标系;
的指向为Ox轴、Oy轴、Oz轴的正方向,建立直角坐标系;

(2)
如图,以底面正方形ABCD的中心为坐标原点O,分别以射线OB、OC、 的指向为Ox轴、Oy轴、Oz轴的正方向,建立直角坐标系.
的指向为Ox轴、Oy轴、Oz轴的正方向,建立直角坐标系.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年上海市宝山区高三上学期期末质量监测数学 题型:解答题
本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
如图,已知正方体 的棱长为2,
的棱长为2, 分别是
分别是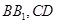 的中点.
的中点.
(1)求三棱锥 的体积;
的体积;
(2)求异面直线EF与AB所成角的大小(结果用反三角函数值表示).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com