
| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 2 | D. | $\sqrt{2}$ |
分析 根据向量加法的平行四边形法则可知$\overrightarrow{BD}=\frac{1}{2}$($\overrightarrow{BA}+\overrightarrow{BC}$).代入$\overrightarrow{BD}•\overrightarrow{BC}$=3即可得出$\overrightarrow{BA}$在$\overrightarrow{BC}$上的投影,根据三角形的性质得出△ABC为等边三角形.
解答 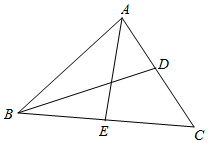 解:∵点D为AC的中点,∴$\overrightarrow{BD}=\frac{1}{2}$($\overrightarrow{BA}+\overrightarrow{BC}$)
解:∵点D为AC的中点,∴$\overrightarrow{BD}=\frac{1}{2}$($\overrightarrow{BA}+\overrightarrow{BC}$)
∴$\overrightarrow{BD}•\overrightarrow{BC}$=$\frac{1}{2}$($\overrightarrow{BA}+\overrightarrow{BC}$)$•\overrightarrow{BC}$=$\frac{1}{2}\overrightarrow{BA}•\overrightarrow{BC}$+$\frac{1}{2}{\overrightarrow{BC}}^{2}$=$\frac{1}{2}\overrightarrow{BA}•\overrightarrow{BC}$+2=3,
∴$\overrightarrow{BA}•\overrightarrow{BC}$=2|$\overrightarrow{BA}$|•cosB=2,
∴|BA|cosB=1,即$\overrightarrow{BA}$在$\overrightarrow{BC}$上的投影为1.
过A作AE⊥BC于E,则BE=1.即E为BC的中点,
∴△ABC是等腰三角形,又∠BAC=60°,
∴△ABC为等边三角形,
∴S△ABC=$\frac{1}{2}×2×2×sin60°$=$\sqrt{3}$.
故选:A.
点评 本题考查了平面向量的数量积运算,平面向量在几何中的应用,属于中档题.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源: 题型:解答题
| 轿车A | 轿车B | |
| 舒适型 | 150 | 400 |
| 标准型 | 450 | 600 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等比数列 | |
| B. | 等差数列 | |
| C. | 等差数列或等比数列 | |
| D. | 可能既不是等差数列也不是等比数列 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
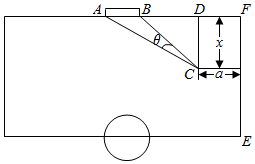 如图,是一块足球训练场地,其中球门AB宽7米,B点位置的门柱距离边线EF的长为21米,现在有一球员在该训练场地进行直线跑动中的射门训练.球员从离底线AF距离x(x≥10)米,离边线EF距离a(7≤a≤14)米的C处开始跑动,跑动线路为CD(CD∥EF),设射门角度∠ACB=θ.
如图,是一块足球训练场地,其中球门AB宽7米,B点位置的门柱距离边线EF的长为21米,现在有一球员在该训练场地进行直线跑动中的射门训练.球员从离底线AF距离x(x≥10)米,离边线EF距离a(7≤a≤14)米的C处开始跑动,跑动线路为CD(CD∥EF),设射门角度∠ACB=θ.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com