
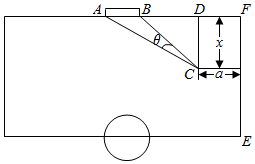
 如图,是一块足球训练场地,其中球门AB宽7米,B点位置的门柱距离边线EF的长为21米,现在有一球员在该训练场地进行直线跑动中的射门训练.球员从离底线AF距离x(x≥10)米,离边线EF距离a(7≤a≤14)米的C处开始跑动,跑动线路为CD(CD∥EF),设射门角度∠ACB=θ.
如图,是一块足球训练场地,其中球门AB宽7米,B点位置的门柱距离边线EF的长为21米,现在有一球员在该训练场地进行直线跑动中的射门训练.球员从离底线AF距离x(x≥10)米,离边线EF距离a(7≤a≤14)米的C处开始跑动,跑动线路为CD(CD∥EF),设射门角度∠ACB=θ.分析 (1)①利用差角的正切函数求出tanθ的值;
②利用函数的单调性,可得球员离底线的距离为多少时,射门角度θ最大;
(2)利用$tanθ=\frac{7x}{{{x^2}+(28-a)(21-a)}}=\frac{1}{3}$,则-x2+21x=a2-49a+28×21,因为7≤a≤14,所以98≤a2-49a+28×21≤294即可求x的取值范围.
解答 解:在△ACD中,设$∠ACD=α,tanα=\frac{AD}{CD}=\frac{AD}{x}$,
在△BCD中,设$∠BCD=β,tanβ=\frac{BD}{CD}=\frac{BD}{x}$,$tanθ=tan(α-β)=\frac{tanα-tanβ}{1+tanαtanβ}=\frac{{\frac{AD}{x}-\frac{BD}{x}}}{{1+\frac{AD}{x}•\frac{BD}{x}}}=\frac{7x}{{{x^2}+AD•BD}}$…(3分)
(1)当a=14时,AD=14,BD=7,
①若x=14,则$tanθ=\frac{7×14}{{{{14}^2}+7×14}}=\frac{1}{3}$; …(6分)
②因为$f(x)=x+\frac{14•7}{x}$在x≥10时单调递增,
所以$tanθ=\frac{7x}{{{x^2}+14•7}}=\frac{7}{{x+\frac{14•7}{x}}}≤\frac{7}{{10+\frac{14•7}{10}}}=\frac{35}{99}$,
所以当x=10时射门角度θ最大; …(10分)
(2)AD=28-a,BD=21-a,
$tanθ=\frac{7x}{{{x^2}+(28-a)(21-a)}}=\frac{1}{3}$,则-x2+21x=a2-49a+28×21…(12分)
因为7≤a≤14,所以98≤a2-49a+28×21≤294,
则98≤-x2+21x≤294,即$\left\{\begin{array}{l}{x^2}-21x+294≥0⇒x∈R\\{x^2}-21x+98≤0⇒7≤x≤14\end{array}\right.$,所以7≤x≤14
又x≥10,所以10≤x≤14
所以x的取值范围是[10,14]. …(15分)
答(1)①当球员离底线的距离x=14时,tanθ的值为$\frac{1}{3}$;
②当球员离底线的距离为10时,射门角度θ最大;
(2)$tanθ=\frac{1}{3}$,则x的取值范围是[10,14]. …(16分)
点评 本题考查函数模型的确立,考查函数的单调性,考查分类讨论的数学思想,考查学生的计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 2 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{2}{5}$+$\frac{4}{5}$i | B. | $\frac{2}{5}$+$\frac{4}{5}$i | C. | $\frac{2}{5}$-$\frac{4}{5}$i | D. | -$\frac{2}{5}$-$\frac{4}{5}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 如果事件A与事件B对立,则P(A)+P(B)=1 | B. | 如果事件A与事件B互斥,则P(A∪B)=1 | ||
| C. | 如果事件A包含于事件B,则P(A)≤P(B) | D. | 如果事件A与事件B相等,则P(A)=P(B) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com