
分析 根据错位相减法即可求出数列的前n项和.
解答 解:Sn=3×($\frac{1}{3}$)1+5×($\frac{1}{3}$)2+7×($\frac{1}{3}$)3+…+(2n+1)($\frac{1}{3}$)n,
$\frac{1}{3}$Sn=3×($\frac{1}{3}$)2+5×($\frac{1}{3}$)3+7×($\frac{1}{3}$)4+…+(2n-1)($\frac{1}{3}$)n+(2n+1)($\frac{1}{3}$)n+1,
两式相减得$\frac{2}{3}$Sn=$\frac{1}{3}$+2×($\frac{1}{3}$)1+2×($\frac{1}{3}$)2+2×($\frac{1}{3}$)3+7×($\frac{1}{3}$)4+…+2×($\frac{1}{3}$)n-(2n+1)($\frac{1}{3}$)n+1,
=$\frac{1}{3}$+2×$\frac{\frac{1}{3}(1-\frac{1}{{3}^{n}})}{1-\frac{1}{3}}$-(2n+1)($\frac{1}{3}$)n+1=$\frac{4}{3}$-(2n+4)($\frac{1}{3}$)n+1,
∴Sn=2-(n+2)($\frac{1}{3}$)n.
点评 本题考查了错位相减法求数列的前n项和,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 等比数列 | |
| B. | 等差数列 | |
| C. | 等差数列或等比数列 | |
| D. | 可能既不是等差数列也不是等比数列 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
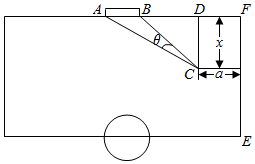 如图,是一块足球训练场地,其中球门AB宽7米,B点位置的门柱距离边线EF的长为21米,现在有一球员在该训练场地进行直线跑动中的射门训练.球员从离底线AF距离x(x≥10)米,离边线EF距离a(7≤a≤14)米的C处开始跑动,跑动线路为CD(CD∥EF),设射门角度∠ACB=θ.
如图,是一块足球训练场地,其中球门AB宽7米,B点位置的门柱距离边线EF的长为21米,现在有一球员在该训练场地进行直线跑动中的射门训练.球员从离底线AF距离x(x≥10)米,离边线EF距离a(7≤a≤14)米的C处开始跑动,跑动线路为CD(CD∥EF),设射门角度∠ACB=θ.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
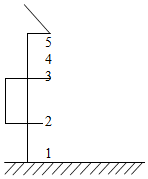 屋檐每隔一定时间滴下一滴水,当第五滴正欲滴下时,第一滴刚好落到地面,而第三滴与第二滴分别位于高1m的窗子的上、下沿,如图所示,g取10m/s2,问:
屋檐每隔一定时间滴下一滴水,当第五滴正欲滴下时,第一滴刚好落到地面,而第三滴与第二滴分别位于高1m的窗子的上、下沿,如图所示,g取10m/s2,问:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com