
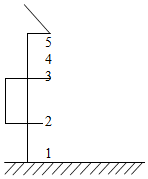
 屋檐每隔一定时间滴下一滴水,当第五滴正欲滴下时,第一滴刚好落到地面,而第三滴与第二滴分别位于高1m的窗子的上、下沿,如图所示,g取10m/s2,问:
屋檐每隔一定时间滴下一滴水,当第五滴正欲滴下时,第一滴刚好落到地面,而第三滴与第二滴分别位于高1m的窗子的上、下沿,如图所示,g取10m/s2,问:分析 (1)可以将这5滴水的运动等效地视为一滴水的下落,并对这一滴水的运动全过程分成4个相等的时间间隔,图中相邻的两滴水间的距离分别对应着各个相等时间间隔内的位移,它们满足比例关系:1:3:5:7.由此能求出此屋檐离地面高度.
(2)由h=gt2,得:t=0.8 s,由此能求出滴水的时间间隔.
解答 解:(1)可以将这5滴水的运动等效地视为一滴水的下落,
并对这一滴水的运动全过程分成4个相等的时间间隔,
图中相邻的两滴水间的距离分别对应着各个相等时间间隔内的位移,
它们满足比例关系:1:3:5:7.
设相邻水滴之间的距离自上而下依次为:x、3x、5x、7x,
则窗户高为5x,
依题意有5x=1m,则x=0.2m.
屋檐高度h=x+3x+5x+7x=16x=3.2 m.
∴此屋檐离地面3.2m.
(2)由h=$\frac{1}{2}$gt2,得t=$\sqrt{\frac{2h}{g}}$=$\sqrt{\frac{2×3.2}{10}}$=0.8(s),
∴滴水的时间间隔△t=$\frac{t}{4}$=$\frac{0.8}{4}$=0.2 s.
点评 本题考查等比数列在生产生活中的实际运用,是中档题,解题时要认真审题,注意等比数列的性质的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | 如果事件A与事件B对立,则P(A)+P(B)=1 | B. | 如果事件A与事件B互斥,则P(A∪B)=1 | ||
| C. | 如果事件A包含于事件B,则P(A)≤P(B) | D. | 如果事件A与事件B相等,则P(A)=P(B) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$共线 | B. | $\overrightarrow{OA}$,$\overrightarrow{OB}$共线 | C. | $\overrightarrow{OB}$,$\overrightarrow{OC}$共线 | D. | O,A,B,C四点共面 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com