
分析 由已知条件利用等比数列通项公式及等差数列性质,列出方程,求出公比为2,由此能求出$\frac{{S}_{4}}{{a}_{2}}$的值.
解答 解:在正项等比数列{an}中2a1,$\frac{1}{2}$a3,a2成等差数列,
∴$\left\{\begin{array}{l}{2×(\frac{1}{2}{a}_{1}{q}^{2})=2{a}_{1}+{a}_{1}q}\\{q>0}\end{array}\right.$,
解得q=2,
∴$\frac{{S}_{4}}{{a}_{2}}$=$\frac{\frac{{a}_{1}(1-{2}^{4})}{1-2}}{{a}_{1}×2}$=$\frac{15}{2}$.
故答案为:$\frac{15}{2}$.
点评 本题考查等比数列的前4项和与第2项的比值的求法,是基础题,解题时要认真审题,注意等比数列、等差数列的性质的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
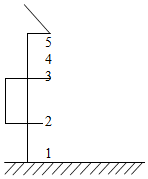 屋檐每隔一定时间滴下一滴水,当第五滴正欲滴下时,第一滴刚好落到地面,而第三滴与第二滴分别位于高1m的窗子的上、下沿,如图所示,g取10m/s2,问:
屋檐每隔一定时间滴下一滴水,当第五滴正欲滴下时,第一滴刚好落到地面,而第三滴与第二滴分别位于高1m的窗子的上、下沿,如图所示,g取10m/s2,问:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 36π | B. | 64π | C. | 144π | D. | 256π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\sqrt{3}$ | B. | $±\sqrt{3}$ | C. | $-\frac{{\sqrt{3}}}{3}$ | D. | $±\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com