
分析 根据函数奇偶性的性质求出当x<0时的解析式,解方程即可.
解答 解:若x<0,则-x>0,
∵定义在R上的奇函数f(x),当x≥0时,f(x)=x2-3x.
∴当x<0时,f(-x)=x2+3x=-f(x).
则当x<0时,f(x)=-x2-3x.
若x≥0,由f(x)=x+3得x2-3x=x+3,
则x2-4x-3=0,则x=$\frac{4±\sqrt{16+4×3}}{2}$=$\frac{4±2\sqrt{7}}{2}$=2±$\sqrt{7}$,
∵x≥0,∴x=2+$\sqrt{7}$,
若x<0,由f(x)=x+3得-x2-3x=x+3,
则x2+4x+3=0,则x=-1或x=-3,
综上方程f(x)=x+3的解集为{2+$\sqrt{7}$,-1,-3};
故答案为:{2+$\sqrt{7}$,-1,-3}
点评 本题主要考查方程根的求解,根据函数奇偶性的性质求出函数的解析式是解决本题的关键.注意要进行分类讨论.


科目:高中数学 来源: 题型:解答题
| 轿车A | 轿车B | |
| 舒适型 | 150 | 400 |
| 标准型 | 450 | 600 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等比数列 | |
| B. | 等差数列 | |
| C. | 等差数列或等比数列 | |
| D. | 可能既不是等差数列也不是等比数列 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
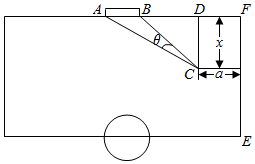 如图,是一块足球训练场地,其中球门AB宽7米,B点位置的门柱距离边线EF的长为21米,现在有一球员在该训练场地进行直线跑动中的射门训练.球员从离底线AF距离x(x≥10)米,离边线EF距离a(7≤a≤14)米的C处开始跑动,跑动线路为CD(CD∥EF),设射门角度∠ACB=θ.
如图,是一块足球训练场地,其中球门AB宽7米,B点位置的门柱距离边线EF的长为21米,现在有一球员在该训练场地进行直线跑动中的射门训练.球员从离底线AF距离x(x≥10)米,离边线EF距离a(7≤a≤14)米的C处开始跑动,跑动线路为CD(CD∥EF),设射门角度∠ACB=θ.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com