
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
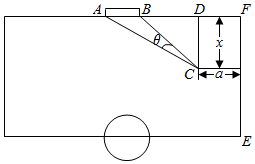 如图,是一块足球训练场地,其中球门AB宽7米,B点位置的门柱距离边线EF的长为21米,现在有一球员在该训练场地进行直线跑动中的射门训练.球员从离底线AF距离x(x≥10)米,离边线EF距离a(7≤a≤14)米的C处开始跑动,跑动线路为CD(CD∥EF),设射门角度∠ACB=θ.
如图,是一块足球训练场地,其中球门AB宽7米,B点位置的门柱距离边线EF的长为21米,现在有一球员在该训练场地进行直线跑动中的射门训练.球员从离底线AF距离x(x≥10)米,离边线EF距离a(7≤a≤14)米的C处开始跑动,跑动线路为CD(CD∥EF),设射门角度∠ACB=θ.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com