
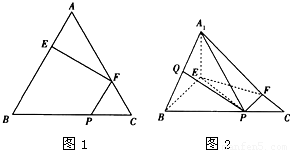
 如图1,在边长为3的正三角形ABC中,E,F,P分别为AB,AC,BC上的点,且满足AE=FC=CP=1.将△AEF沿EF折起到△A1EF的位置,使平面A1EF⊥平面EFB,连接A1B,A1P.(如图2)
如图1,在边长为3的正三角形ABC中,E,F,P分别为AB,AC,BC上的点,且满足AE=FC=CP=1.将△AEF沿EF折起到△A1EF的位置,使平面A1EF⊥平面EFB,连接A1B,A1P.(如图2)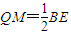 ,进一步可得QM∥PF,且QM=PF,从而四边形PQMF为平行四边形,可得PQ∥FM,利用线面平行的判定,可得PQ∥平面A1EF;
,进一步可得QM∥PF,且QM=PF,从而四边形PQMF为平行四边形,可得PQ∥FM,利用线面平行的判定,可得PQ∥平面A1EF; 证明:(Ⅰ)取A1E中点M,连接QM,MF.
证明:(Ⅰ)取A1E中点M,连接QM,MF. .
.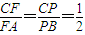 ,
, ,
, (Ⅱ) 取BE中点D,连接DF.
(Ⅱ) 取BE中点D,连接DF.

 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:
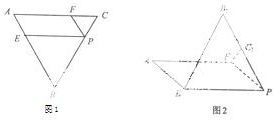 如图1,在边长为3的正三角形ABC中,E、F、P分别是AB、AC、BC边上的点,满足AE=CF=CP=1,今将△BEP、△CFP分别沿EP、FP向上折起,使边BP与边CP所在的直线重合(如图2),B、C折后的对应点分别记为B、C1.
如图1,在边长为3的正三角形ABC中,E、F、P分别是AB、AC、BC边上的点,满足AE=CF=CP=1,今将△BEP、△CFP分别沿EP、FP向上折起,使边BP与边CP所在的直线重合(如图2),B、C折后的对应点分别记为B、C1.查看答案和解析>>
科目:高中数学 来源: 题型:
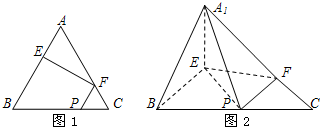 如图1,在边长为3的正三角形ABC中,E,F,P分别为AB,AC,
如图1,在边长为3的正三角形ABC中,E,F,P分别为AB,AC,查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•东城区一模)如图1,在边长为3的正三角形ABC中,E,F,P分别为AB,AC,BC上的点,且满足AE=FC=CP=1.将△AEF沿EF折起到△A1EF的位置,使平面A1EF⊥平面EFB,连接A1B,A1P.(如图2)
(2012•东城区一模)如图1,在边长为3的正三角形ABC中,E,F,P分别为AB,AC,BC上的点,且满足AE=FC=CP=1.将△AEF沿EF折起到△A1EF的位置,使平面A1EF⊥平面EFB,连接A1B,A1P.(如图2)查看答案和解析>>
科目:高中数学 来源: 题型:
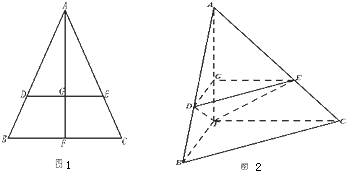 如图1,在边长为3的等边三角形ABC中,D,E分别是AB,AC边上的点,AD=AE,F是BC的中点,AF与DE交于点G,将△ABF沿AF折起,得到如图2所示的三棱锥A-BCF,其中BC=
如图1,在边长为3的等边三角形ABC中,D,E分别是AB,AC边上的点,AD=AE,F是BC的中点,AF与DE交于点G,将△ABF沿AF折起,得到如图2所示的三棱锥A-BCF,其中BC=3
| ||
| 2 |
| 2 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com