
【题目】设A、B分别为双曲线 ![]() 的左右顶点,双曲线的实轴长为4
的左右顶点,双曲线的实轴长为4 ![]() ,焦点到渐近线的距离为
,焦点到渐近线的距离为 ![]() .
.
(1)求双曲线的方程;
(2)已知直线 ![]() 与双曲线的右支交于M、N两点,且在双曲线的右支上存在点D,使
与双曲线的右支交于M、N两点,且在双曲线的右支上存在点D,使 ![]() ,求t的值及点D的坐标.
,求t的值及点D的坐标.
【答案】
(1)解:由实轴长为 ![]() ,得
,得 ![]() ,
,
渐近线方程为 ![]() x,即bx﹣2
x,即bx﹣2 ![]() y=0,
y=0,
∵焦点到渐近线的距离为 ![]() ,
,
∴ ![]() ,又c2=b2+a2,∴b2=3,
,又c2=b2+a2,∴b2=3,
∴双曲线方程为: ![]()
(2)解:设M(x1,y1),N(x2,y2),D(x0,y0),则x1+x2=tx0,y1+y2=ty0,
由 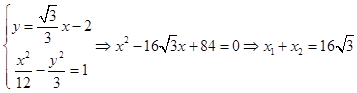 ,
,
∴y1+y2= ![]() ﹣4=12,
﹣4=12,
∴ 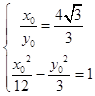 ,解得
,解得 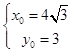 ,∴t=4,
,∴t=4,
∴ ![]() ,t=4
,t=4
【解析】(1)由实轴长可得a值,由焦点到渐近线的距离可得b,c的方程,再由a,b,c间的平方关系即可求得b;(2)设M(x1 , y1),N(x2 , y2),D(x0 , y0),则x1+x2=tx0 , y1+y2=ty0 , 则x1+x2=tx0 , y1+y2=ty0 , 联立直线方程与双曲线方程消掉y得x的二次方程,由韦达定理可得x1+x2 , 进而求得y1+y2 , 从而可得 ![]() ,再由点D在双曲线上得一方程,联立方程组即可求得D点坐标,从而求得t值;
,再由点D在双曲线上得一方程,联立方程组即可求得D点坐标,从而求得t值;


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:
【题目】已知△ABC的三个内角A,B,C所对的边分别为a,b,c,∠A是锐角,且 ![]() b=2asinB.
b=2asinB.
(1)求∠A的度数;
(2)若a=7,△ABC的面积为10 ![]() ,求b2+c2的值.
,求b2+c2的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高一年级学生中随机抽取60名学生,将其期中考试的数学成绩(均为整数)分成六段:[40,50),[50,60),…,[90,100]后得到如下频率分布直方图. 
(1)求分数在[70,80)内的频率;
(2)根据频率分布直方图,估计该校高一年级学生期中考试数学成绩的平均分;
(3)用分层抽样的方法在80分以上的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任意选取2人,求其中恰有1人的分数不低于90分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC中,a、b、c分别为角A、B、C所在的对边,且a=4,b+c=5,tanB+tanC+ ![]() =
= ![]() tanBtanC,则△ABC的面积为( )
tanBtanC,则△ABC的面积为( )
A.![]()
B.3 ![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,已知a+b=5,c= ![]() ,且4sin2
,且4sin2 ![]() ﹣cos2C=
﹣cos2C= ![]()
(1)求角C的大小;
(2)求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知P为△ABC内一点,且满足 ![]() ,记△ABP,△BCP,△ACP的面积依次为S1 , S2 , S3 , 则S1:S2:S3等于( )
,记△ABP,△BCP,△ACP的面积依次为S1 , S2 , S3 , 则S1:S2:S3等于( )
A.1:2:3
B.1:4:9
C.2:3:1
D.3:1:2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cosωxsin(ωx﹣ ![]() )+
)+ ![]() cos2ωx﹣
cos2ωx﹣ ![]() (ω>0,x∈R),且函数y=f(x)图象的一个对称中心到它对称轴的最近距离为
(ω>0,x∈R),且函数y=f(x)图象的一个对称中心到它对称轴的最近距离为 ![]() .
.
(1)求ω的值及f(x)的对称轴方程;
(2)在△ABC中,角A,B,C的对边分别为a,b,c,若f(A)=0,sinB= ![]() ,a=
,a= ![]() ,求b的值.
,求b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com