
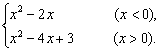 求f{f[f(-4)]};?
求f{f[f(-4)]};? (2)已知f(x)=x2-1,?g(x)=![]() 求f(g(x))与g(f(x)).?
求f(g(x))与g(f(x)).?
解:(1)∵-4<0,?∴f(-4)=(-4)+4=0.?
∴f(f(-4))=f(0)=1.于是f{f[f(-4)]}=f(f(0))=f(1)=12+3=4.?
(2)当x>0时,g(x)=2-x,f(g(x))=(2-x)2-1=x2-4x+3.?
当x<0时,g(x)=x-1,f(g(x))=(x-1)2-1=x2-2x,故f(g(x))=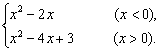
当x2-1<0,即-1<x<1时,f(x)<0,所以g(f(x))=f(x)-1=x2-2.?
当x2-1>0,即x>1或x<-1时,f(x)<0,
所以g(f(x))=2-f(x)=3-x2.?
故g(f(x))=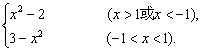
点评:本题涉及分段函数和复合函数的综合问题,注意分析自变量取不同值时,对函数解析式的选取.一般地,分段函数的复合函数仍然是分段函数.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
(1)已知f(x)=x2+2x,求f(2x+1);
(2)已知f(![]() -1)=x+2
-1)=x+2![]() ,求f(x);
,求f(x);
(3)已知f(x)-![]() )=3x+2,求f(x).
)=3x+2,求f(x).
查看答案和解析>>
科目:高中数学 来源: 题型:
(2)已知f(x)满足f(x-![]() )=x2+
)=x2+![]() ,求函数f(x)的解析式;
,求函数f(x)的解析式;
(3)已知函数f(x)是一次函数,且f[f(x)]=4x+1,求函数f(x)的解析式.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省无为县四高三考文科数学试卷(解析版) 题型:解答题
(本题满分12分)设函数f(x)=x3- ax2+3x+5(a>0).
ax2+3x+5(a>0).
(1)已知f(x)在R上是单调函数,求a的取值范围;
(2)若a=2,且当x∈[1,2]时,f(x)≤m恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010年辽宁省庄河市高一上学期第一次月考数学卷 题型:解答题
(本题12分)(1)已知f (x+1)=x2+4x+1,求f (x)的解析式;
(2)已知f ( )=
)= +1,求f (x) 的解析式. (不必写出定义域)
+1,求f (x) 的解析式. (不必写出定义域)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com