
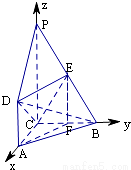
(12分)如图,DA⊥平面ABC,DA∥PC,∠ACB=90°,AC=AD=BC=1,PC=2,E为PB的中点.

(Ⅰ)求证:DE∥平面ABC;
(Ⅱ)求二面角E﹣CD﹣B的余弦值.
(Ⅰ)详见解析;(Ⅱ)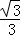 .
.
【解析】
试题分析:(Ⅰ)取BC的中点F,连结EF,AF,要证DE∥平面ABC,只要证DE∥AF,即只要证四边形ADEF是平行四边形即可;
(Ⅱ)分别以CA,CB,CP所在的直线分别为x轴,y轴,z轴,建立空间坐标系如图,根据题设写出相关点的坐标,并利用向量的坐标运算求出平面ECD和平面BCD的法向量,进而利用向的夹角公式求解.
试题解析:【解析】
(1)取BC的中点F,连结EF,
则EF∥PC∥DA,且EF= PC=DA=1,
PC=DA=1,
则四边形ADEF是平行四边形,
即DE∥AF,
∵DE平面ABC,AF平面ABC,
∴DE∥平面ABC;
(2)∵DA⊥平面ABC,DA∥PC,
∴PC⊥平面ABC,
∵∠ACB=90°,AC=AD=BC=1,PC=2,
∴分别以CA,CB,CP所在的直线分别为x轴,y轴,z轴,建立空间坐标系如图,
则A(1,0,0),B(0,1,0),D(1,0,1),P(0,0,2),
则E(0, ,1),则
,1),则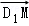 =(1,0,﹣1),
=(1,0,﹣1),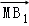 =(1,2,1),
=(1,2,1),
设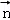 =(x,y,z)是平面ECD的法向量,
=(x,y,z)是平面ECD的法向量,
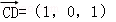 ,
,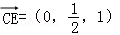 ,
,
则 ,
,
令z=1,则x=﹣1,y=﹣2,则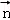 =(﹣1,﹣2,1),
=(﹣1,﹣2,1),
设 =(x,y,z)是平面BCD的法向量,
=(x,y,z)是平面BCD的法向量,
∵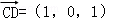 ,
, ,
,
∴ ,
,
令z=1,则x=﹣1,则 =(﹣1,0,1),
=(﹣1,0,1),
∴cos< >=
>=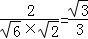 .
.
易知二面角E﹣CD﹣B为锐角,
故二面角E﹣CD﹣B的余弦值为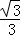 .
.
考点:1、空间直线与平面的位置关系;2、空间向量法在解决立体几何问题中的应用.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源:2014-2015学年广西梧州、崇左两市联考高三上学期摸底文科数学试卷(解析版) 题型:解答题
在直角坐标系xOy中,以原点O为极点,x轴的非负半轴为极轴建立极坐标系,已知圆C的圆心的极坐标为( ,
, ),半径r=
),半径r= ,点P的极坐标为(2,π),过P作直线l交圆C于A,B两点.
,点P的极坐标为(2,π),过P作直线l交圆C于A,B两点.
(1)求圆C的直角坐标方程;
(2)求|PA||PB|的值.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广西梧州、崇左两市联考高三上学期摸底文科数学试卷(解析版) 题型:选择题
执行如图所示的程序框图,输出的k值为( )
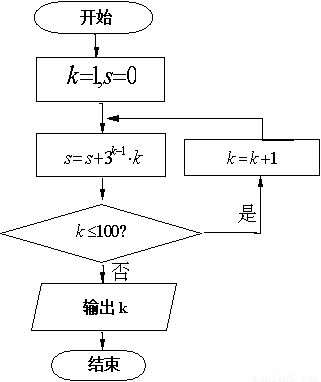
A.3 B.4 C.5 D.6
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广西梧州、崇左两市联考高三上学期摸底理科数学试卷(解析版) 题型:解答题
在直角坐标系xOy中,以原点O为极点,x轴的非负半轴为极轴建立极坐标系,已知圆C的圆心的极坐标为(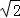 ,
, ),半径r=
),半径r=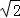 ,点P的极坐标为(2,π),过P作直线l交圆C于A,B两点.
,点P的极坐标为(2,π),过P作直线l交圆C于A,B两点.
(1)求圆C的直角坐标方程;(2)求|PA||PB|的值.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广西梧州、崇左两市联考高三上学期摸底理科数学试卷(解析版) 题型:填空题
若曲线y=aln(x+1)在点(0,0)处的切线方程为y=2x,则a= _________ .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广西梧州、崇左两市联考高三上学期摸底理科数学试卷(解析版) 题型:选择题
执行如图所示的程序框图,输出的k值为( )

A.3 B.4 C.5 D.6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com