
【题目】已知四棱柱![]() 的底面是边长为2的菱形,且
的底面是边长为2的菱形,且![]() ,
,![]() ⊥平面
⊥平面![]() ,
,![]() ,设
,设![]() 为
为![]() 的中点.
的中点.

(1)求证:![]() ⊥平面
⊥平面![]() ;
;
(2)点![]() 在线段
在线段![]() 上,且
上,且![]() 平面
平面![]() ,求平面
,求平面![]() 和平面
和平面![]() 所成锐角的余弦值.
所成锐角的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)由侧棱![]() 可知,该棱柱为直四棱柱,所以
可知,该棱柱为直四棱柱,所以![]() 且交线为
且交线为![]() ,又底面
,又底面![]() 为菱形且
为菱形且![]() ,所以
,所以![]() 为等比三角形,由于
为等比三角形,由于![]() 为
为![]() 中点,所以
中点,所以![]() ,所以
,所以![]() ,所以
,所以![]() ,又根据侧面
,又根据侧面![]() 为矩形,且
为矩形,且![]() ,
,![]() ,所以
,所以![]() 为等腰直角三角形,即
为等腰直角三角形,即![]() ,又因为
,又因为![]() ,所以
,所以![]() ;(2)取
;(2)取![]() 中点
中点![]() ,连接
,连接![]() ,由
,由![]() 为等比三角形易知
为等比三角形易知![]() ,则
,则![]() ,以
,以![]() 所在直线分别为
所在直线分别为![]() 轴建立如图的空间直角坐标系,根据第(1)问可知,
轴建立如图的空间直角坐标系,根据第(1)问可知,![]() 为平面
为平面![]() 的法向量,由于
的法向量,由于![]() 平面
平面![]() ,所以
,所以![]() ,于是可以求出点
,于是可以求出点![]() 的坐标,然后求出平面
的坐标,然后求出平面![]() 的法向量
的法向量![]() ,将平面
,将平面![]() 与平面
与平面![]() 所成角的余弦转化成两个法向量成角余弦值,即可求解.
所成角的余弦转化成两个法向量成角余弦值,即可求解.
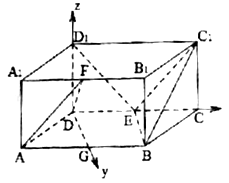
试题解析:(1)证明:由已知该四棱柱为直四棱柱,且△![]() 为等边三角形,
为等边三角形,![]() ⊥
⊥![]() ,
,
所以![]() ⊥平面
⊥平面![]() ,故
,故![]() ⊥
⊥![]() .
.
因为△![]() 的三边长分别为
的三边长分别为![]() ,
,![]() ,故△
,故△![]() 为等腰直角三角形,
为等腰直角三角形,
所以![]() ⊥
⊥![]() ,结合
,结合![]() ⊥
⊥![]() 知:
知:![]() ⊥平面
⊥平面![]() .
.
(2)解:取![]() 中点
中点![]() ,则由△
,则由△![]() 为等边三角形知
为等边三角形知![]() ⊥
⊥![]() ,从而
,从而![]() ⊥
⊥![]() .
.
以![]() ,
,![]() ,
,![]() 为坐标轴,建立如图所示的坐标系,此时
为坐标轴,建立如图所示的坐标系,此时![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .设
.设![]() ,
,
由上面的讨论知平面![]() 的法向量为
的法向量为![]() ,
,
由于![]() 平面
平面![]() ,故
,故![]() 平面
平面![]() ,所以
,所以![]() ,故
,故![]() ,
,
故![]() ,所以
,所以![]() ,故
,故![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,![]() ,
,![]() ,
,
由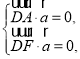 知
知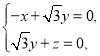 取
取![]() ,
,![]() ,
,![]() ,故
,故![]() .
.
设平面![]() 和平面
和平面![]() 所成锐角为
所成锐角为![]() ,则
,则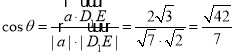 ,
,
即平面![]() 和平面
和平面![]() 所成锐角的余弦值为
所成锐角的余弦值为![]() .
.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
【题目】平潭国际“花式风筝冲浪”集训队,在平潭龙凤头海滨浴场进行集训,海滨区域的某个观测点观测到该处水深![]() (米)是随着一天的时间
(米)是随着一天的时间![]() 呈周期性变化,某天各时刻
呈周期性变化,某天各时刻![]() 的水深数据的近似值如下表:
的水深数据的近似值如下表:
| 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| 1.5 | 2.4 | 1.5 | 0.6 | 1.4 | 2.4 | 1.6 | 0.6 | 1.5 |
(Ⅰ)根据表中近似数据画出散点图(坐标系在答题卷中).观察散点图,从
①![]() , ②
, ②![]() ,③
,③![]()
![]() 中选择一个合适的函数模型,并求出该拟合模型的函数解析式;(Ⅱ)为保证队员安全,规定在一天中的5~18时且水深不低于1.05米的时候进行训练,根据(Ⅰ) 中的选择的函数解析式,试问:这一天可以安排什么时间段组织训练,才能确保集训队员的安全。
中选择一个合适的函数模型,并求出该拟合模型的函数解析式;(Ⅱ)为保证队员安全,规定在一天中的5~18时且水深不低于1.05米的时候进行训练,根据(Ⅰ) 中的选择的函数解析式,试问:这一天可以安排什么时间段组织训练,才能确保集训队员的安全。
查看答案和解析>>
科目:高中数学 来源: 题型:
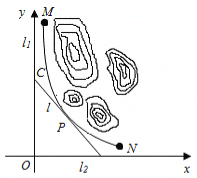
【题目】 某山区外围有两条相互垂直的直线型公路,为进一步改善山区的交通现状,计划修建一条连接两条公路的山区边界的直线型公路,记两条相互垂直的公路为![]() ,山区边界曲线为
,山区边界曲线为![]() ,计划修建的公路为
,计划修建的公路为![]() ,如图所示,
,如图所示,![]() 为
为![]() 的两个端点,测得点
的两个端点,测得点![]() 到
到![]() 的距离分别为5千米和40千米,点
的距离分别为5千米和40千米,点![]() 到
到![]() 的距离分别为20千米和2.5千米,以
的距离分别为20千米和2.5千米,以![]() 所在的直线分别为
所在的直线分别为![]() 轴,建立平面直角坐标系
轴,建立平面直角坐标系![]() ,假设曲线
,假设曲线![]() 符合函数
符合函数![]() (其中
(其中![]() 为常数)模型.
为常数)模型.
(1)求![]() 的值;
的值;
(2)设公路![]() 与曲线
与曲线![]() 相切于
相切于![]() 点,
点,![]() 的横坐标为
的横坐标为![]() .
.
①请写出公路![]() 长度的函数解析式
长度的函数解析式![]() ,并写出其定义域;
,并写出其定义域;
②当![]() 为何值时,公路
为何值时,公路![]() 的长度最短?求出最短长度.
的长度最短?求出最短长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在长方体![]() 中,
中,![]() ,
,![]() 是棱
是棱![]() 上的一点.
上的一点.
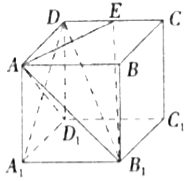
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() ;
;
(3)若![]() 是棱
是棱![]() 的中点,在棱
的中点,在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出线段
?若存在,求出线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() ,且
,且![]() 在
在![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围;
的取值范围;
(2)是否存在实数![]() ,使得函数
,使得函数![]() 在
在![]() 上的最小值为1?若存在,求出实数
上的最小值为1?若存在,求出实数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(A)设函数![]() ,
, ![]() .
.
(1)证明:函数![]() 在
在![]() 上为增函数;
上为增函数;
(2)若方程![]() 有且只有两个不同的实数根,求实数
有且只有两个不同的实数根,求实数![]() 的值.
的值.
(B)已知函数![]() .
.
(1)求函数![]() 的最小值;
的最小值;
(2)若存在唯一实数![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() ,
, ![]() 是椭圆
是椭圆![]() 的右焦点,
的右焦点, ![]() 的斜率为
的斜率为![]() ,
, ![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)设过点![]() 的动直线
的动直线![]() 与
与![]() 交于
交于![]() ,
, ![]() 两点,当
两点,当![]() 面积最大时,求
面积最大时,求![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:极坐标与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)求曲线![]() 的普通方程;
的普通方程;
(2)经过点![]() (平面直角坐标系
(平面直角坐标系![]() 中点)作直线
中点)作直线![]() 交曲线
交曲线![]() 于
于![]() ,
, ![]() 两点,若
两点,若![]() 恰好为线段
恰好为线段![]() 的三等分点,求直线
的三等分点,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数
,函数![]() .
.
(1)求证:曲线![]() 在点
在点![]() 处的切线过定点;
处的切线过定点;
(2)若![]() 是
是![]() 在区间
在区间![]() 上的极大值,但不是最大值,求实数
上的极大值,但不是最大值,求实数![]() 的取值范围;
的取值范围;
(3)求证:对任意给定的正数![]() ,总存在
,总存在![]() ,使得
,使得![]() 在
在![]() 上为单调函数.
上为单调函数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com