
【题目】已知函数![]() .
.

(1)若函数![]() 是偶函数.求
是偶函数.求![]() 的值,并在坐标系中画出
的值,并在坐标系中画出![]() 的大致图象;
的大致图象;
(2)若当![]() 时,
时,![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】类比三角形中的性质:(1)两边之和大于第三边;(2)中位线长等于底边的一半;(3)三内角平分线交于一点; 可得四面体的对应性质:(1)任意三个面的面积之和大于第四个面的面积;(2)过四面体的交于同一顶点的三条棱的中点的平面面积等于第四个面面积的![]() ;(3)四面体的六个二面角的平分面交于一点。其中类比推理结论正确的有 ( )
;(3)四面体的六个二面角的平分面交于一点。其中类比推理结论正确的有 ( )
A. (1) B. (1)(2) C. (1)(2)(3) D. 都不对
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣1+alnx.(e为自然对数的底数),λ=min{a+2,5}.(min{a,b}表示a,b中较小的数.)
(1)当a=0时,设g(x)=f(x)﹣x,求函数g(x)在[![]() ,
,![]() ]上的最值;
]上的最值;
(2)当x![]() 1时,证明:f(x)+x2
1时,证明:f(x)+x2![]() λ(x﹣1)+2.
λ(x﹣1)+2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某渔业公司今年初用98万元购进一艘远洋渔船,每年的捕捞可有50万元的总收入,已知使用![]() 年(
年(![]() )所需(包括维修费)的各种费用总计为
)所需(包括维修费)的各种费用总计为![]() 万元.
万元.
(1)该船捞捕第几年开始赢利(总收入超过总支出,今年为第一年)?
(2)该船若干年后有两种处理方案:
①当赢利总额达到最大值时,以8万元价格卖出;
②当年平均赢利达到最大值时,以26万元卖出,问哪一种方案较为合算?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】挑选空间飞行员可以说是“万里挑一”,要想通过需要五关:目测、初检、复检、文考(文化考试)、政审.若某校甲、乙、丙三位同学都顺利通过了前两关,根据分析甲、乙、丙三位同学通过复检关的概率分别是0.5、0.6、0.75,能通过文考关的概率分别是0.6、0.5、0.4,由于他们平时表现较好,都能通过政审关,若后三关之间通过与否没有影响.
(1)求甲被录取成为空军飞行员的概率;
(2)求甲、乙、丙三位同学中恰好有一个人通过复检的概率;
(3)设只要通过后三关就可以被录取,求录取人数![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对两个变量y和x进行回归分析,则下列说法中不正确的是( )
A.由样本数据得到的回归方程![]() 必过样本点的中心
必过样本点的中心![]() .
.
B.残差平方和越小的模型,拟合的效果越好.
C.用相关指数![]() 来刻画回归效果,
来刻画回归效果,![]() 的值越小,说明模型的拟合效果越好.
的值越小,说明模型的拟合效果越好.
D.回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法.
查看答案和解析>>
科目:高中数学 来源: 题型:
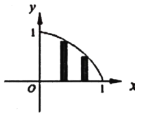
【题目】在平面直角坐标系中,函数![]() 在第一象限内的图像如图所示,试做如下操作,把
在第一象限内的图像如图所示,试做如下操作,把![]() 轴上的区间
轴上的区间![]() 等分成
等分成![]() 个小区间,在每一个小区间上作一个小矩形,使矩形的右端点落在函数
个小区间,在每一个小区间上作一个小矩形,使矩形的右端点落在函数![]() 的图像上.若用
的图像上.若用![]() ,表示第
,表示第![]() 个矩形的面积,
个矩形的面积,![]() 表示这
表示这![]() 个矩形的面积总和.
个矩形的面积总和.
(Ⅰ)求![]() 的表达式;
的表达式;
(Ⅱ)请用数学归纳法证明等式:![]() ;
;
(Ⅲ)求![]() 的值,并说明
的值,并说明![]() 的几何意义.
的几何意义.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com