
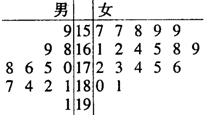
 2013��8��28��-30�գ�������ԥ�̴���ڡ�����֮Դ������֮�����������о��У�Ϊ�˸�ýӴ������������ί����ijѧԺ��ļ��12����־Ը�ߺ�18��Ů־Ը�ߣ�����30��־Ը�ߵ����߱������ʾ�ľ�Ҷͼ����λ��cm������������175cm���ϣ�����175cm������Ϊ���߸��ӡ���������175cm���£�������175cm������Ϊ���Ǹ߸��ӡ�����ֻ�С�Ů�߸��ӡ��ŵ��Ρ�����С�㡱��
2013��8��28��-30�գ�������ԥ�̴���ڡ�����֮Դ������֮�����������о��У�Ϊ�˸�ýӴ������������ί����ijѧԺ��ļ��12����־Ը�ߺ�18��Ů־Ը�ߣ�����30��־Ը�ߵ����߱������ʾ�ľ�Ҷͼ����λ��cm������������175cm���ϣ�����175cm������Ϊ���߸��ӡ���������175cm���£�������175cm������Ϊ���Ǹ߸��ӡ�����ֻ�С�Ů�߸��ӡ��ŵ��Ρ�����С�㡱������ �����ȸ��ݸ��ݾ�Ҷͼ��������߸��ӡ������Ǹ߸��ӡ����������÷ֲ�����ķ��������ÿ���˱����еĸ��ʣ��Ӷ����ѡ�еġ��߸��ӡ������Ǹ߸��ӡ�����������������Ӧ�ĸ��ʣ�
����������ã�X=0��1��2��3��������Ӧ�ĸ��ʣ��Ӷ�д��X�ķֲ��У�X����ѧ������
��� �⣺�����ݾ�Ҷͼ���С��߸��ӡ�12�ˣ����Ǹ߸��ӡ�18�ˣ�
�÷ֲ�����ķ�����ÿ���˱����еĸ�����$\frac{5}{30}$=$\frac{1}{6}$��
��ѡ�еġ��߸��ӡ���12��$\frac{1}{6}$=2�ˣ����Ǹ߸��ӡ���18��$\frac{1}{6}$=3�ˣ�
���¼�A��ʾ��������һ���߸��ӱ�ѡ�С���
�����Ķ����¼�$\overline{A}$��ʾ��û��һ���߸��ӱ�ѡ�С���
��P��A��=1-P��$\overline{A}$��=1-$\frac{{C}_{3}^{2}}{{C}_{5}^{2}}$=1-$\frac{3}{10}$=$\frac{7}{10}$��
��������һ���ǡ��߸��ӡ��ĸ�����$\frac{7}{10}$��
����������ã�X=0��1��2��3��
P����=0��=$\frac{{C}_{8}^{3}}{{C}_{12}^{3}}$=$\frac{14}{55}$��P����=1��=$\frac{{{C}_{4}^{1}C}_{8}^{2}}{{C}_{12}^{3}}$=$\frac{28}{55}$��
P����=2��=$\frac{{{C}_{4}^{2}C}_{8}^{1}}{{C}_{12}^{3}}$=$\frac{12}{55}$��P����=3��=$\frac{{C}_{4}^{3}}{{C}_{12}^{3}}$=$\frac{1}{55}$��
��εķֲ������£�
| �� | 0 | 1 | 2 | 3 |
| P | $\frac{14}{55}$ | $\frac{28}{55}$ | $\frac{12}{55}$ | $\frac{1}{55}$ |
���� ���⿼������ɢ����������������ͷ��������һ���е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | 3 | C�� | 2 | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
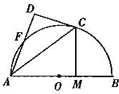 ��ͼ��AB��ԲO��ֱ����C��FΪԲO�ϵ㣬CA�ǡ�BAF�Ľ�ƽ���ߣ�CD��ԲO���ڵ�C�ҽ�AF���ӳ����ڵ�D��CM��AB������Ϊ��M����֤��
��ͼ��AB��ԲO��ֱ����C��FΪԲO�ϵ㣬CA�ǡ�BAF�Ľ�ƽ���ߣ�CD��ԲO���ڵ�C�ҽ�AF���ӳ����ڵ�D��CM��AB������Ϊ��M����֤���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �٢� | B�� | �٢ۢ� | C�� | �ڢۢ� | D�� | �٢� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com