
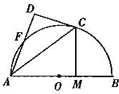
 如图,AB是圆O的直径,C、F为圆O上点,CA是∠BAF的角平分线,CD与圆O切于点C且交AF的延长线于点D,CM⊥AB,垂足为点M,求证:
如图,AB是圆O的直径,C、F为圆O上点,CA是∠BAF的角平分线,CD与圆O切于点C且交AF的延长线于点D,CM⊥AB,垂足为点M,求证:分析 (1)由CA是∠BAF的角平分线推理出OC∥AD,DC是圆O的切线,所以CD⊥OC,则CD⊥AD;
(2)由圆的切割线定理得到DC=CM,求出DF•AM的值.
解答 解:(1)连接OC,则有∠OAC=∠OCA.
又CA是∠BAF的角平分线,∠OAC=∠FAC,所以∠FAC=∠ACO,所以OC∥AD.
因为DC是圆O的切线,所以CD⊥OC,则CD⊥AD.
(2)由题意知△AMC≌△ADC,所以DC=CM,DA=AM.
因为DC是圆O的切线,由切割线定理,得DC2=DF•DA=DF•AM=CM2.
在Rt△ABC中,AC=AB•cos∠BAC=$\sqrt{3}$,
所以CM=$\frac{1}{2}$AC=$\frac{\sqrt{3}}{2}$.
于是DF•AM=CM2=$\frac{3}{4}$.
点评 本题主要考查平面几何证明中圆的基本性质的应用,考查切割线定理,属于中档题.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | log22015 | B. | 2015 | C. | -2015 | D. | 1008 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 80 | C. | -80 | D. | -32 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
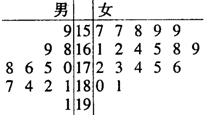 2013年8月28日-30日,第六届豫商大会在“三商之源、华商之都”的商丘市举行,为了搞好接待工作,大会组委会在某学院招募了12名男志愿者和18名女志愿者,将这30名志愿者的身高编成如所示的茎叶图(单位:cm).若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有“女高个子”才担任“礼仪小姐”.
2013年8月28日-30日,第六届豫商大会在“三商之源、华商之都”的商丘市举行,为了搞好接待工作,大会组委会在某学院招募了12名男志愿者和18名女志愿者,将这30名志愿者的身高编成如所示的茎叶图(单位:cm).若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有“女高个子”才担任“礼仪小姐”.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({\frac{7π}{12},0})$ | B. | $({\frac{π}{3},0})$ | C. | $({\frac{11π}{6},0})$ | D. | $({\frac{3π}{2},0})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com