
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
分析 根据题意和向量的数量积化简$|\overrightarrow{a}+\overrightarrow{b}{|}^{2}+|\overrightarrow{a}-\overrightarrow{b}{|}^{2}=2(|\overrightarrow{a}{|}^{2}+|\overrightarrow{b}{|}^{2})$,求出向量$\overrightarrow{a},\overrightarrow{b}$的关系,再将式子$\sqrt{3}$|$\overrightarrow{a}+\overrightarrow{b}$|=$\sqrt{3}$|$\overrightarrow{a}$|两边平方,化简后可求出向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角.
解答 解:∵|$\overrightarrow{a}-\overrightarrow{b}$|=$\sqrt{3}$|$\overrightarrow{a}+\overrightarrow{b}$|=$\sqrt{3}$|$\overrightarrow{a}$|,且$|\overrightarrow{a}+\overrightarrow{b}{|}^{2}+|\overrightarrow{a}-\overrightarrow{b}{|}^{2}=2(|\overrightarrow{a}{|}^{2}+|\overrightarrow{b}{|}^{2})$,
∴$|\overrightarrow{a}{|}^{2}+3|\overrightarrow{a}{|}^{2}=2(|\overrightarrow{a}{|}^{2}+|\overrightarrow{b}{|}^{2})$,化简可得,$|\overrightarrow{a}|=|\overrightarrow{b}|$,
由$\sqrt{3}$|$\overrightarrow{a}+\overrightarrow{b}$|=$\sqrt{3}$|$\overrightarrow{a}$|得,|$\overrightarrow{a}+\overrightarrow{b}$|=|$\overrightarrow{a}$|,
两边平方可得,${\overrightarrow{a}}^{2}+2\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}={\overrightarrow{a}}^{2}$,
∴cos<$\overrightarrow{a},\overrightarrow{b}$>=$-\frac{1}{2}$,则向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角是$\frac{2π}{3}$,
故选:D.
点评 本题考查向量的数量积运算的综合应用,以及结论:$|\overrightarrow{a}+\overrightarrow{b}{|}^{2}+|\overrightarrow{a}-\overrightarrow{b}{|}^{2}=2(|\overrightarrow{a}{|}^{2}+|\overrightarrow{b}{|}^{2})$,属于中档题.


科目:高中数学 来源: 题型:解答题
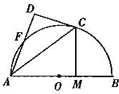 如图,AB是圆O的直径,C、F为圆O上点,CA是∠BAF的角平分线,CD与圆O切于点C且交AF的延长线于点D,CM⊥AB,垂足为点M,求证:
如图,AB是圆O的直径,C、F为圆O上点,CA是∠BAF的角平分线,CD与圆O切于点C且交AF的延长线于点D,CM⊥AB,垂足为点M,求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com