
分析 (Ⅰ)由题知$y=\frac{{{e^{ax}}}}{x}$在[1,+∞)上为增函数,则将题目转化成ax-1≥0在[1,+∞)上恒成立,
(Ⅱ)对参数m讨论,利用g(x)的单调性求解.
(Ⅲ)由(Ⅱ)知,当x>0时,g(x)在(0,2)上单调递减,在(2,+∞)上单调递增,故$g(x)≥g(2)=\frac{e}{2}$,即$\frac{{{e^{\frac{x}{2}}}}}{x}≥\frac{e}{2}$,列式求解即可.
解答 解:(Ⅰ)由题知$y=\frac{{{e^{ax}}}}{x}$在[1,+∞)上为增函数,
故$(\frac{{{e^{ax}}}}{x})'=\frac{{{e^{ax}}(ax-1)}}{x^2}≥0$在[1,+∞)上恒成立,故ax-1≥0在[1,+∞)上恒成立,
即$a≥\frac{1}{x}$在x∈[1,+∞)上恒成立,而$\frac{1}{x}≤1$,∴a≥1.--------------(4分)
(Ⅱ)当$a=\frac{1}{2}$时,$g(x)=\frac{f(x)}{x}=\frac{{{e^{\frac{x}{2}}}}}{x}$,$g'(x)=\frac{{{e^{\frac{x}{2}}}(\frac{x}{2}-1)}}{x^2}$,--------------(5分)
当x>2时,g'(x)>0,即g(x)在[2,+∞)上单调递增;
当x<2且x≠0时,g'(x)<0,即g(x)在(0,2),(-∞,0)上单调递减;
又m>0,∴m+1>1
故当m≥2时,g(x)在[m,m+1]上单调递增,此时$g{(x)_{min}}=g(m)=\frac{{{e^{\frac{m}{2}}}}}{m}$;
当0<m≤1时,m+1≤2,g(x)在[m,m+1]上单调递减,此时$g{(x)_{min}}=g(m+1)=\frac{{{e^{\frac{m+1}{2}}}}}{m+1}$;
当1<m<2时,g(x)在[m,2]上单调递减,在[2,m+1]单调递增,故此时$g{(x)_{min}}=g(2)=\frac{e}{2}$;--------------(8分)
综上有:当0<m≤1时,$g{(x)_{min}}=g(m+1)=\frac{{{e^{\frac{m+1}{2}}}}}{m+1}$;
当1<m<2时,$g{(x)_{min}}=g(2)=\frac{e}{2}$;
当m≥2时,$g{(x)_{min}}=g(m)=\frac{{{e^{\frac{m}{2}}}}}{m}$.--------------(9分)
(Ⅲ)由(Ⅱ)知,当x>0时,g(x)在(0,2)上单调递减,在(2,+∞)上单调递增,
故$g(x)≥g(2)=\frac{e}{2}$,即$\frac{{{e^{\frac{x}{2}}}}}{x}≥\frac{e}{2}$,---------------(10分)
故当x>0时,总有$\frac{x}{{{e^{\frac{x}{2}}}}}≤\frac{2}{e}$成立,
取x=n时有$\frac{n}{{{{(\sqrt{e})}^n}}}≤\frac{2}{e}$,$\frac{1}{{n{{(\sqrt{e})}^n}}}=\frac{n}{{{n^2}{{(\sqrt{e})}^n}}}≤\frac{1}{n^2}•\frac{2}{e}$,--------------(12分)
故$\frac{1}{{\sqrt{e}}}+\frac{1}{{2{{(\sqrt{e})}^2}}}+\frac{1}{{3{{(\sqrt{e})}^3}}}+…+\frac{1}{{n{{(\sqrt{e})}^n}}}≤\frac{2}{e}(1+\frac{1}{2^2}+\frac{1}{3^2}+…+\frac{1}{n^2})$$<\frac{2}{e}(\frac{5}{4}+\frac{1}{2×3}+\frac{1}{3×4}+…+\frac{1}{(n-1)n})=\frac{2}{e}(\frac{5}{4}+\frac{1}{2}-\frac{1}{n})<\frac{7}{2e}$.--------------(14分)
点评 本题主要考查了利用导数求参数的取值范围,和利用导数证明不等式的成立,属于难度较大题型,在高考中常作压轴出现.


科目:高中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{a=3}\\{b=-3}\end{array}\right.$或$\left\{\begin{array}{l}{a=-4}\\{b=11}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{a=-4}\\{b=11}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{a=-1}\\{b=5}\end{array}\right.$ | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱柱ABCD-A1B1C1D1中,AB=BC=CA=$\sqrt{3}$,AD=CD=AA1=1,平面AA1C1C⊥平面ABCD,E为线段BC的中点,
如图,在四棱柱ABCD-A1B1C1D1中,AB=BC=CA=$\sqrt{3}$,AD=CD=AA1=1,平面AA1C1C⊥平面ABCD,E为线段BC的中点,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 时间x | 1 | 2 | 3 | 4 | 5 |
| 命中率y | 0.4 | 0.5 | 0.6 | 0.6 | 0.4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
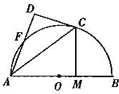 如图,AB是圆O的直径,C、F为圆O上点,CA是∠BAF的角平分线,CD与圆O切于点C且交AF的延长线于点D,CM⊥AB,垂足为点M,求证:
如图,AB是圆O的直径,C、F为圆O上点,CA是∠BAF的角平分线,CD与圆O切于点C且交AF的延长线于点D,CM⊥AB,垂足为点M,求证:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com