一个正方体的六个面上分别标有A,B,C,D,E,F.下图是正方体的两种不同放置.则与D面相对的面上的字母是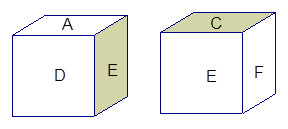题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

一个正方体的六个面上分别标有A,B,C,D,E,F，下图是正方体的两种不同放置，则与D面相对的面上的字母是________

解析试题分析：根据两个图形的字母，结合模型，可推断出来，A对面是C；B对面是E；则与D面相对的面上的字母是 F．
考点：本题主要考查正方体的几何特征，推理判断能力。
点评：简单题，结合模型作出判断。

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：填空题

下面是空间线面位置关系中传递性的部分相关命题：
①与两条平行线中一条平行的平面必与另一条直线平行；
②与两条平行线中一条垂直的平面必与另一条直线垂直；
③与两条垂直直线中一条平行的平面必与另一条直线垂直；
④与两条垂直直线中一条垂直的平面必与另一条直线平行；
⑤与两个平行平面中一个平行的直线必与另一个平面平行；
⑥与两个平行平面中一个垂直的直线必与另一个平面垂直；
⑦与两个垂直平面中一个平行的直线必与另一个平面垂直；
⑧与两个垂直平面中一个垂直的直线必与另一个平面平行.
其中正确的命题个数有________个.

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

空间直角坐标系中，已知A（1，0，2），B（1，－3，1），点P在z轴上，且|PA|=|PB|,则点P的坐标为 .

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

将正方形ABCD沿对角线BD折成直二面角A－BD－C，有如下四个结论：
①AC⊥BD； ②△ACD是等边三角形；
③AB与平面BCD成60°的角； ④AB与CD所成的角是60°.
其中正确结论的序号是________．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

正三棱锥P—ABC中，CM=2PM，CN=2NB，对于以下结论：

①二面角B—PA—C大小的取值范围是（，π）；
②若MN⊥AM，则PC与平面PAB所成角的大小为；
③过点M与异面直线PA和BC都成的直线有3条；
④若二面角B—PA—C大小为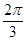，则过点N与平面PAC和平面PAB都成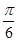的直线有3条．
正确的序号是．