
将正方形ABCD沿对角线BD折成直二面角A-BD-C,有如下四个结论:
①AC⊥BD; ②△ACD是等边三角形;
③AB与平面BCD成60°的角; ④AB与CD所成的角是60°.
其中正确结论的序号是________.
①②④
解析试题分析:①取BD的中点O,连接OA,OC,所以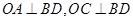 ,所以
,所以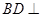 平面OAC,所以AC⊥BD;②设正方形的边长为a,则在直角三角形ACO中,可以求得OC=a,
平面OAC,所以AC⊥BD;②设正方形的边长为a,则在直角三角形ACO中,可以求得OC=a,
所以△ACD是等边三角形;③AB与平面BCD成45角;④分别取BC,AC的中点为M,N,连接ME,NE,MN.则MN∥AB,且MN=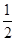 AB=
AB=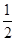 a,ME∥CD,且ME=
a,ME∥CD,且ME=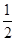 CD=
CD=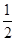 a,∴∠EMN是异面直线AB,CD所成的角.在Rt△AEC中,AE=CE=
a,∴∠EMN是异面直线AB,CD所成的角.在Rt△AEC中,AE=CE=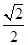 a,AC=a,∴NE=
a,AC=a,∴NE=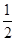 AC=
AC=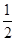 a.∴△MEN是正三角形,∴∠EMN=60°,故④正确.
a.∴△MEN是正三角形,∴∠EMN=60°,故④正确.
考点:本小题主要考查平面图形向空间图形的折叠问题,考查学生的空间想象能力.
点评:解决此类折叠问题,关键是搞清楚折叠前后的变量和不变的量.


科目:高中数学 来源: 题型:填空题
在平面几何里,有勾股定理:“设△ABC的两边AB,AC互相垂直,则AB2+AC2=BC2.”拓展到空间,类比平面几何的勾股定理,研究三棱锥的面面积与底面面积间的关系。可以得出的正确结论是:“设三棱锥A—BCD的三个侧面ABC、ACD、ADB两两相互垂直,则 ”.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com