练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

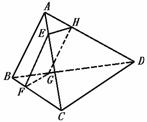
     如图，四边形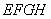为四面体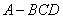 的一个截面，若截面为平行四边形，

    求证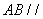：平面


    证明：∵EFGH为平行四边形，∴EF∥HG，

    ∵HG平面ABD，∴EF∥平面ABD.

    ∵EF平面ABC，平面ABD∩平面ABC＝AB.

    ∴EF∥AB，∴AB∥平面EFGH.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

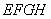
    科目：高中数学 来源：2014-2015学年福建省高一下学期第一次月考数学试卷（解析版） 题型：选择题

    某工厂甲、乙、丙三个车间生产了同一种产品，数量分别为120件、80件、60件．为了解它们的产品质量是否存在显著差别，用分层抽样方法抽取了一个容量为n的样本进行调查，其中从丙车间的产品中抽取了3件，则n＝( )

    A．9 B．10 C．12 D．13

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    正三棱柱的高为，底面边长为，则它的体积为       ，它的侧面积为        ，它的表面积为      

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某几何体的三视图如图所示，则该几何体的体积是（    ）

    A．     B．    C．      D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某几何体的三视图如图所示，则该几何体的表面积为（    ）

                                                                                

    A．  B．   C．    D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某几何体的三视图如图1所示，它的体积为(     )

                                         

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，是圆的直径，垂直于圆所在的平面，是圆上的点．

    （1）求证:平面；

    （2）设为的中点，为的重心，求证：平面∥平面．

     


    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知四棱锥 (图5) 的三视图如图6所示，为正三角形，垂直底面，俯视图是直角梯形．（1）求正视图的面积；（2）求四棱锥的体积；（3）求证：平面；

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数．

    （Ⅰ）求函数的单调递增区间；

    （Ⅱ）若关于的方程在区间内恰有两个相异的实根，求实数的取值范围．

    查看答案和解析>>

    同步练习册答案