
| A. | 90 | B. | 100 | C. | 110 | D. | 120 |
分析 由题意可得4S3=3(a3+7),4S2=2(a2+a3),4S1=a1+a2,运用数列的递推式可得a1=1,a2=3,a3=5,进而得到an=2n-1,${S_n}={n^2}$,即可得到所求值.
解答 解:由数列{an}的前n项和为Sn,a4=7且4Sn=n(an+an+1),
可得4S3=3(a3+7),4S2=2(a2+a3),4S1=a1+a2,
∴a2=3a1,a3=5a1,
从而4×9a1=3(5a1+7),
即a1=1,∴a2=3,a3=5,
∴4S4=4(a4+a5),
∴a5=9,同理得a7=13,a8=15,…,an=2n-1,
∴${S_n}={n^2}$,经验证4Sn=n(an+an+1)成立,
∴S10=100.
故选:B.
点评 本题考查数列的通项公式和前n项和的求法,注意运用数列递推式,考查化简整理的运算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | (¬p)∨q | C. | p∨(¬q) | D. | (¬p)∧(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
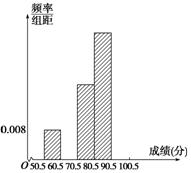 为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示),解答下列问题:
为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示),解答下列问题:| 分组 | 频数 | 频率 |
| 50.5~60.5 | 4 | 0.08 |
| 60.5~70.5 | 0.16 | |
| 70.5~80.5 | 10 | |
| 80.5~90.5 | 16 | 0.32 |
| 90.5~100.5 | ||
| 合计 | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1.4 | B. | 3.0 | C. | 3.6 | D. | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±x | B. | y=±$\sqrt{2}$x | C. | y=±2x | D. | y=±$\frac{\sqrt{2}}{2}$x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com