练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图1-4-12,已知CD是Rt△ABC的斜边AB上的高线.求证:CD·AC=BC·AD.

    图1-4-12

    思路分析:分别在三个直角三角形Rt△ABC、Rt△ADC、Rt△BDC中运用射影定理，有CD2=BD·AD,BC2=BD·AB,AC2=AD·AB，将第一个式子和第三个式子相乘，就有CD2·?AC2=BD·AB·AD2，将BD·AB换成BC2，然后两边开方即得.

    证明：∵CD是Rt△ABC的斜边AB上的高线，?

    ∴CD2=BD·AD,BC2=BD·AB,AC2=AD·AB.?

    ∴CD2·AC2=BD·AB·AD2,BC2=BD·AB.?

    ∴CD2·AC2=BC2·AD2.?

    ∴CD·AC=BC·AD.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    如图1-4-12,已知△ABC的面积为 60 cm2,D为BC上一点,且BD∶DC=1∶3,E、F是AC和AB上的点,四边形EFDC的面积等于△BCE的面积，求△ABE的面积.

    图1-4-12

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年广东省肇庆市高三数学复习必修2模块测试试卷D卷 题型：解答题

    (12分) 如图7-4，已知△ABC中， ∠ACB=90°，CD⊥AB，且AD=1，BD=2，△ACD绕CD旋转至A′CD，使点A′与点B之间的距离A′B=。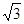

     

     

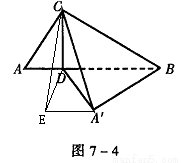
    （1）求证：BA′⊥平面A′CD；

    （2）求二面角A′－CD－B的大小；

    （3）求异面直线A′C与BD所成的角的余弦值。

     

    查看答案和解析>>

    科目：高中数学 来源：2014届河南省高一下学期第一次月考数学试卷 题型：解答题

    学校开展的综合实践活动中，某班进行了小制作评比，作品上交时间为5月1日至30日，评委会把同学们上交作品的件数按5天一组分组统计，绘制了频率分布直方图(如图所示)，已知从左到右各长方形的高的比为2：3：4：6：4：1，第三组的频数为12，请解答下列问题：

    (1)本次活动共有多少件作品参加评比?

    (2)哪组上交的作品数最多?有多少件?

    (3)经过评比，第4组和第6组分别有10件、2件作品获奖，这两组 哪 组获奖率较高?

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图1-4-12,已知CD是Rt△ABC的斜边AB上的高线，求证:CD·AC=BC·AD.

    图1-4-12

    查看答案和解析>>

    同步练习册答案