
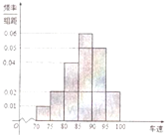
 我州某高中一研究性学习小组,在某一告诉公路服务区进行社会实践活动,从小型汽车中按进服务区的先后,每间隔5辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段:[70,75),[75,80),[80,85),[85,90),[90,95),[95,100),统计后得到如图的频率分布直方图.
我州某高中一研究性学习小组,在某一告诉公路服务区进行社会实践活动,从小型汽车中按进服务区的先后,每间隔5辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段:[70,75),[75,80),[80,85),[85,90),[90,95),[95,100),统计后得到如图的频率分布直方图.分析 (1)每间隔5辆就抽取一辆的抽样方法抽取样本数据,符合系统抽样的特征,可得用到的抽样方法是系统抽样;
由小矩形最高的是[85,90)组,可得样本数据的众数为$\frac{85+90}{2}$,0.01×5+0.02×5+0.04×5=0.35<0.5,设0.01×5+0.02×5+0.04×5+0.06×m=0.5,解得m.
(2)车速在[70,80)的车辆共有6辆,车速在[70,75)和[75,80)的车辆分别有2辆和4辆,若从车速在[70,80)的车辆中任意抽取3辆,车速在[75,80)的车辆数为x,则x的可能取值为1,2,3,利用超几何分布列计算公式即可得出.
解答 解:(1)∵每间隔5辆就抽取一辆的抽样方法抽取样本数据,符合系统抽样的特征,∴在采样中,用到的抽样方法是系统抽样;
∵小矩形最高的是[85,90)组,∴样本数据的众数为$\frac{85+90}{2}$=87.5.
∵0.01×5+0.02×5+0.04×5=0.35<0.5,设0.01×5+0.02×5+0.04×5+0.06×m=0.5,则m=2.5,
∴中位数的估计值为85+m=87.5;…(6分)
(2)车速在[70,80)的车辆共有6辆,车速在[70,75)和[75,80)的车辆
分别有2辆和4辆,若从车速在[70,80)的车辆中任意抽取3辆,车速在[75,80)的车辆数为x,则x的可能取值为1,2,3;
∴P(x=1)=$\frac{{∁}_{2}^{2}•{∁}_{4}^{1}}{{∁}_{6}^{3}}$=$\frac{1}{5}$,P(x=2)=$\frac{{∁}_{2}^{1}{∁}_{4}^{2}}{{∁}_{6}^{3}}$=$\frac{3}{5}$,
P(x=3)=$\frac{{∁}_{2}^{0}{∁}_{4}^{3}}{{∁}_{6}^{3}}$=$\frac{1}{5}$,
∴分布列为:
| X | 1 | 2 | 3 |
| P | $\frac{1}{5}$ | $\frac{3}{5}$ | $\frac{1}{5}$ |
点评 本题考查了频率分布直方图、超几何分布列计算公式及其数学期望,考查了推理能力与计算能力,属于中档题.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
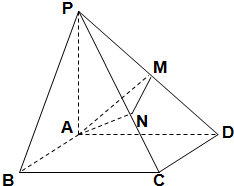 四棱锥P-ABCD的底面是矩形,PA⊥平面ABCD,且PA=AD=2AB,点M,N分别在侧棱PD,PC上,且$\overrightarrow{PM}=\overrightarrow{MD}$.
四棱锥P-ABCD的底面是矩形,PA⊥平面ABCD,且PA=AD=2AB,点M,N分别在侧棱PD,PC上,且$\overrightarrow{PM}=\overrightarrow{MD}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{ln2}{2}$ | C. | ln2 | D. | 1-ln2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
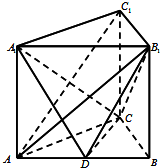 如图,三棱柱ABC-A1B1C1侧棱垂直于底面,AB=4,AC=BC=3,D为AB的中点.
如图,三棱柱ABC-A1B1C1侧棱垂直于底面,AB=4,AC=BC=3,D为AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com