
| A. | $\frac{1}{2}$ | B. | $\frac{ln2}{2}$ | C. | ln2 | D. | 1-ln2 |
分析 由关于x的方程ax2+2x+c=0有实根,得ac≤1,由此能求出x的方程ax2+2x+c=0有实根的概率.
解答 解:∵关于x的方程ax2+2x+c=0有实根,
∴判别式△=4-4ac≥0,解得ac≤1,
∵A={(a,c)|1≤a≤2,0≤c≤1,a,c∈R},则任取(a,c)∈A,
∴基本事件总数为:xy=1,
满足关于x的方程ax2+2x+c=0有实根的基本事件个数为:${∫}_{1}^{2}\frac{1}{x}dx$=ln2,
∴x的方程ax2+2x+c=0有实根的概率为p=$\frac{ln2}{1}$=ln2.
故选:C.
点评 本题考查概率的求法,是中档题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
| X | 0 | 1 | 2 | 3 |
| P | $\frac{1}{8}$ | $\frac{3}{8}$ | $\frac{3}{8}$ | a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
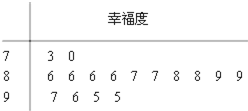 某权威机构发布了2014年度“城市居民幸福排行榜”,某市成为本年度城市最“幸福城”.随后,该市某校学生会组织部分同学,用“10分制”随机调查“阳光”社区人们的幸福度.现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):
某权威机构发布了2014年度“城市居民幸福排行榜”,某市成为本年度城市最“幸福城”.随后,该市某校学生会组织部分同学,用“10分制”随机调查“阳光”社区人们的幸福度.现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):查看答案和解析>>
科目:高中数学 来源: 题型:解答题
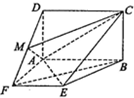 如图,四边形ABCD是矩形,BC⊥平面ABEF,四边形ABEF是梯形,∠EFA=∠FAB=90°,EF=FA=AD=1,点M是DF的中点,AB=2.
如图,四边形ABCD是矩形,BC⊥平面ABEF,四边形ABEF是梯形,∠EFA=∠FAB=90°,EF=FA=AD=1,点M是DF的中点,AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
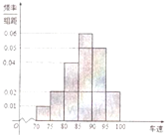 我州某高中一研究性学习小组,在某一告诉公路服务区进行社会实践活动,从小型汽车中按进服务区的先后,每间隔5辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段:[70,75),[75,80),[80,85),[85,90),[90,95),[95,100),统计后得到如图的频率分布直方图.
我州某高中一研究性学习小组,在某一告诉公路服务区进行社会实践活动,从小型汽车中按进服务区的先后,每间隔5辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段:[70,75),[75,80),[80,85),[85,90),[90,95),[95,100),统计后得到如图的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com