
分析 (1)利用绝对值三角不等式,结合基本不等式,即可证明;
(2)若f(3)<5,即|3+$\frac{4}{a}$|+|3-a|<5,进而$\frac{4}{a}$-2<a-3<2-$\frac{4}{a}$,即可求出实数a的取值范围.
解答 (1)证明:f(x)=|x+$\frac{4}{a}$|+|x-a|≥|$\frac{4}{a}$+a|=|$\frac{4}{a}$|+|a|≥2$\sqrt{|\frac{4}{a}||a|}$=4;
(2)解:若f(3)<5,即|3+$\frac{4}{a}$|+|3-a|<5,
∵a>0,∴3+$\frac{4}{a}$+|3-a|<5,
∴|3-a|<2-$\frac{4}{a}$,
∴$\frac{4}{a}$-2<a-3<2-$\frac{4}{a}$,
∴1<a<4.
点评 本题考查绝对值三角不等式,基本不等式的运用,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
 如图,60°的二面角棱上有A′,B′两点,直线AA′,BB′分别在这个二面角的半平面内,且都垂直于A′B′,已知A′B′=3,AA′=3,BB′=5,则AB的长度为2$\sqrt{7}$.
如图,60°的二面角棱上有A′,B′两点,直线AA′,BB′分别在这个二面角的半平面内,且都垂直于A′B′,已知A′B′=3,AA′=3,BB′=5,则AB的长度为2$\sqrt{7}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{ln2}{2}$ | C. | ln2 | D. | 1-ln2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
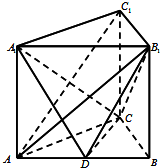 如图,三棱柱ABC-A1B1C1侧棱垂直于底面,AB=4,AC=BC=3,D为AB的中点.
如图,三棱柱ABC-A1B1C1侧棱垂直于底面,AB=4,AC=BC=3,D为AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | -$\frac{3}{4}$ | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{2}$,1) | B. | ($\frac{1}{2}$,1] | C. | [$\frac{\sqrt{3}}{2}$,1) | D. | ($\frac{\sqrt{3}}{2}$,1] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com