
 如图,60°的二面角棱上有A′,B′两点,直线AA′,BB′分别在这个二面角的半平面内,且都垂直于A′B′,已知A′B′=3,AA′=3,BB′=5,则AB的长度为2$\sqrt{7}$.
如图,60°的二面角棱上有A′,B′两点,直线AA′,BB′分别在这个二面角的半平面内,且都垂直于A′B′,已知A′B′=3,AA′=3,BB′=5,则AB的长度为2$\sqrt{7}$. 分析 由已知得${\overrightarrow{AB}}^{2}$=($\overrightarrow{A{A}^{'}}+\overrightarrow{{A}^{'}{B}^{'}}+\overrightarrow{{B}^{'}B}$)2=${\overrightarrow{A{A}^{'}}}^{2}+{\overrightarrow{{A}^{'}{B}^{'}}}^{2}+{\overrightarrow{{B}^{'}B}}^{2}$+2|$\overrightarrow{A{A}^{'}}$|×|$\overrightarrow{{B}^{'}B}$|×cos120°,由此能求出AB的长度.
解答 解:∵60°的二面角棱上有A′,B′两点,
直线AA′,BB′分别在这个二面角的半平面内,且都垂直于A′B′,
A′B′=3,AA′=3,BB′=5,
∴${\overrightarrow{AB}}^{2}$=($\overrightarrow{A{A}^{'}}+\overrightarrow{{A}^{'}{B}^{'}}+\overrightarrow{{B}^{'}B}$)2=${\overrightarrow{A{A}^{'}}}^{2}+{\overrightarrow{{A}^{'}{B}^{'}}}^{2}+{\overrightarrow{{B}^{'}B}}^{2}$+2|$\overrightarrow{A{A}^{'}}$|×|$\overrightarrow{{B}^{'}B}$|×cos120°
=9+9+25-2×$3×5×\frac{1}{2}$=28,
∴AB的长度为|$\overrightarrow{AB}$|=2$\sqrt{7}$.
故答案为:2$\sqrt{7}$.
点评 本题考查空间中两点间距离的求法,是中档题,解题时要认真审题,注意向量法的合理运用.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:解答题
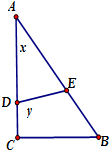 如图,在直角三角形ABC中,∠ACB=90°,AC=4,BC=3,点D,E分别线段AC,AB上,线段DE分三角形ABC为面积相等的两部分,设AD=x,DE=y.
如图,在直角三角形ABC中,∠ACB=90°,AC=4,BC=3,点D,E分别线段AC,AB上,线段DE分三角形ABC为面积相等的两部分,设AD=x,DE=y.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| X | 0 | 1 | 2 | 3 |
| P | $\frac{1}{8}$ | $\frac{3}{8}$ | $\frac{3}{8}$ | a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
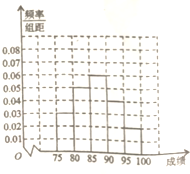 某高中毕业学年,在高校自主招生期间,把学生的平时成绩按“百分制”折算,排出前100名学生,并对这100名学生按成绩分组(从低到高依次分为第1组、第2组、第3组、第4组、第5组),其频率分布直方图如图:现Q大学决定在第3、4、5组中用分层抽样的方法抽取6名学生进行面试,且本次面试中有B、C、D三位考官.
某高中毕业学年,在高校自主招生期间,把学生的平时成绩按“百分制”折算,排出前100名学生,并对这100名学生按成绩分组(从低到高依次分为第1组、第2组、第3组、第4组、第5组),其频率分布直方图如图:现Q大学决定在第3、4、5组中用分层抽样的方法抽取6名学生进行面试,且本次面试中有B、C、D三位考官.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
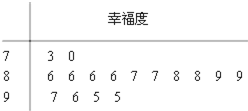 某权威机构发布了2014年度“城市居民幸福排行榜”,某市成为本年度城市最“幸福城”.随后,该市某校学生会组织部分同学,用“10分制”随机调查“阳光”社区人们的幸福度.现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):
某权威机构发布了2014年度“城市居民幸福排行榜”,某市成为本年度城市最“幸福城”.随后,该市某校学生会组织部分同学,用“10分制”随机调查“阳光”社区人们的幸福度.现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com