
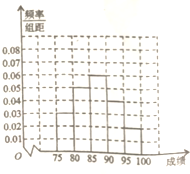
 某高中毕业学年,在高校自主招生期间,把学生的平时成绩按“百分制”折算,排出前100名学生,并对这100名学生按成绩分组(从低到高依次分为第1组、第2组、第3组、第4组、第5组),其频率分布直方图如图:现Q大学决定在第3、4、5组中用分层抽样的方法抽取6名学生进行面试,且本次面试中有B、C、D三位考官.
某高中毕业学年,在高校自主招生期间,把学生的平时成绩按“百分制”折算,排出前100名学生,并对这100名学生按成绩分组(从低到高依次分为第1组、第2组、第3组、第4组、第5组),其频率分布直方图如图:现Q大学决定在第3、4、5组中用分层抽样的方法抽取6名学生进行面试,且本次面试中有B、C、D三位考官.分析 (1)利用互斥事件及相互独立事件的概率公式求解;
(2)由图得到每一组学生的人数,由分层抽样求得第三、四、五组分别抽取的人数,可得ξ的取值情况,求出概率,得到分布列,再由期望公式求得期望.
解答 解:(1)设事件A=甲同学测试成功.
则P(A)=$\frac{1}{2}×\frac{1}{3}×\frac{3}{4}+\frac{1}{2}×\frac{2}{3}×\frac{1}{4}+\frac{1}{2}×\frac{1}{3}×\frac{1}{4}+\frac{1}{2}×\frac{1}{3}×\frac{1}{4}=\frac{7}{24}$;
(2)∵总人数为100人,由直方图可知,第一组人数为15人,第二组人数为25人,第三组人数为30人,
第四组人数为20人,第五组人数为10人,第三、四、五组中用分层抽样的方法抽取6名学生进行面试,
则第三、四、五组分别抽取3人、2人、1人,
由题意得ξ=0、1、2,
P(ξ=0)=$\frac{{C}_{2}^{0}{C}_{4}^{2}}{{C}_{6}^{3}}=\frac{1}{5}$,P(ξ=0)=$\frac{{C}_{2}^{1}{C}_{4}^{2}}{{C}_{6}^{3}}=\frac{3}{5}$,P(ξ=0)=$\frac{{C}_{2}^{2}{C}_{4}^{1}}{{C}_{6}^{3}}=\frac{1}{5}$.
分布列为
| ξ | 0 | 1 | 2 |
| p | $\frac{1}{5}$ | $\frac{3}{5}$ | $\frac{1}{5}$ |
点评 本题考查离散型随机变量的期望与方差,考查学生读取图表的能力,是中档题.


 优等生题库系列答案
优等生题库系列答案科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{π}{4}$个单位 | B. | 向左平移$\frac{π}{4}$个单位 | ||
| C. | 向左平移$\frac{π}{2}$个单位 | D. | 向右平移$\frac{π}{2}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点.
如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{9}$ | D. | $\frac{4}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,60°的二面角棱上有A′,B′两点,直线AA′,BB′分别在这个二面角的半平面内,且都垂直于A′B′,已知A′B′=3,AA′=3,BB′=5,则AB的长度为2$\sqrt{7}$.
如图,60°的二面角棱上有A′,B′两点,直线AA′,BB′分别在这个二面角的半平面内,且都垂直于A′B′,已知A′B′=3,AA′=3,BB′=5,则AB的长度为2$\sqrt{7}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
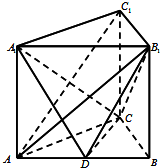 如图,三棱柱ABC-A1B1C1侧棱垂直于底面,AB=4,AC=BC=3,D为AB的中点.
如图,三棱柱ABC-A1B1C1侧棱垂直于底面,AB=4,AC=BC=3,D为AB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com