
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{9}$ | D. | $\frac{4}{9}$ |
分析 由题意知ξ的取值有0,1,2,当ξ=0时,表示的事件是A邮箱的信件数为0,由分步计数原理知两封信随机投入A、B、C三个空邮箱,共有3×3种结果,而满足条件的A邮箱的信件数为0的结果数是2×2,由古典概型公式得到ξ=0时的概率,同理可得ξ=1时,ξ=2时的概率,用期望公式得到结果
解答 解:A邮筒中信件数X可能为0,1,2.
则P(X=0)=$\frac{2×2}{3×3}$=$\frac{4}{9}$,P(X=1)=$\frac{4}{9}$,P(X=2)=$\frac{1}{9}$,
其分布列为:
| X | 0 | 1 | 2 |
| P | $\frac{4}{9}$ | $\frac{4}{9}$ | $\frac{1}{9}$ |
点评 本题考查了古典概率计算公式及其随机变量的数学期望,考查了分类讨论方法、推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| X | 0 | 1 | 2 | 3 |
| P | $\frac{1}{8}$ | $\frac{3}{8}$ | $\frac{3}{8}$ | a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
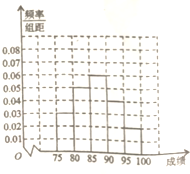 某高中毕业学年,在高校自主招生期间,把学生的平时成绩按“百分制”折算,排出前100名学生,并对这100名学生按成绩分组(从低到高依次分为第1组、第2组、第3组、第4组、第5组),其频率分布直方图如图:现Q大学决定在第3、4、5组中用分层抽样的方法抽取6名学生进行面试,且本次面试中有B、C、D三位考官.
某高中毕业学年,在高校自主招生期间,把学生的平时成绩按“百分制”折算,排出前100名学生,并对这100名学生按成绩分组(从低到高依次分为第1组、第2组、第3组、第4组、第5组),其频率分布直方图如图:现Q大学决定在第3、4、5组中用分层抽样的方法抽取6名学生进行面试,且本次面试中有B、C、D三位考官.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
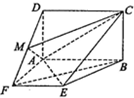 如图,四边形ABCD是矩形,BC⊥平面ABEF,四边形ABEF是梯形,∠EFA=∠FAB=90°,EF=FA=AD=1,点M是DF的中点,AB=2.
如图,四边形ABCD是矩形,BC⊥平面ABEF,四边形ABEF是梯形,∠EFA=∠FAB=90°,EF=FA=AD=1,点M是DF的中点,AB=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com