
分析 (Ⅰ)设甲第一次抛掷大于等于3点为事件A,乙第一次抛掷大于等于3点为事件B,甲第二次抛掷大于等于3点为事件C,可得P(A)=P(B)=P(C)=$\frac{2}{3}$,P($\overline{A}$)=P($\overline{B}$)=P($\overline{C}$)=$\frac{1}{3}$.再由相互独立事件的概率求得前3次抛掷甲得2分且乙得1分的概率;
(Ⅱ)由题意求得ξ的取值,进一步求得对应的概率,得到分布列,代入期望公式求得数学期望.
解答 解:(Ⅰ)设甲第一次抛掷大于等于3点为事件A,乙第一次抛掷大于等于3点为事件B,甲第二次抛掷大于等于3点为事件C.
则P(A)=P(B)=P(C)=$\frac{2}{3}$,P($\overline{A}$)=P($\overline{B}$)=P($\overline{C}$)=$\frac{1}{3}$.
前3次抛掷甲得2分且乙得1分包括甲两次均大于等于3点乙大于等于3点;甲有1次不大于等于3点乙的1次不大于等于3点.
∴前3次抛掷甲得2分且乙得1分的概率P=$(P(A))^{2}P(B)+{C}_{2}^{1}P(A)P(\overline{A})P(\overline{B})$=$(\frac{2}{3})^{2}×\frac{2}{3}+2×\frac{2}{3}×\frac{1}{3}×\frac{1}{3}=\frac{4}{9}$;
(Ⅱ)ξ=0、1、2、3.
P(ξ=0)=$\frac{2}{3}×\frac{2}{3}×\frac{1}{3}=\frac{4}{27}$,P(ξ=1)=$\frac{4}{9}$,P(ξ=2)=$\frac{1}{3}$,P(ξ=3)=$\frac{1}{3}×\frac{2}{3}×\frac{1}{3}=\frac{2}{27}$.
分布列为:
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{4}{27}$ | $\frac{4}{9}$ | $\frac{1}{3}$ | $\frac{2}{27}$ |
点评 本题考查离散型随机变量的期望与方差,考查了独立重复试验与相互独立事件的概率,是中档题.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
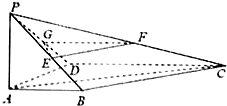 已知如图,四边形ABCD是直角梯形,AB∥DC,AB⊥AD,AP⊥平面ABCD,DC=2AB=2AD=2AP,点E、F、G分别是PB、PC、PD的中点.
已知如图,四边形ABCD是直角梯形,AB∥DC,AB⊥AD,AP⊥平面ABCD,DC=2AB=2AD=2AP,点E、F、G分别是PB、PC、PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
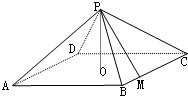 如图:四棱锥P-ABCD中,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=$\frac{π}{3}$,M是BC上的点,且BM=$\frac{1}{2}$,
如图:四棱锥P-ABCD中,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=$\frac{π}{3}$,M是BC上的点,且BM=$\frac{1}{2}$,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{9}$ | D. | $\frac{4}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
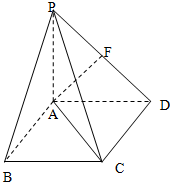 如图,四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是边长为2的正方形,PA=AD,F为PD的中点.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是边长为2的正方形,PA=AD,F为PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
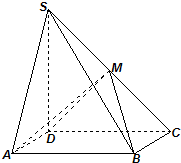 如图,四棱锥S-ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD=$\sqrt{2}$,DC=SD=2,点M是侧棱SC的中点.
如图,四棱锥S-ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD=$\sqrt{2}$,DC=SD=2,点M是侧棱SC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com