
ΓΨΧβΡΩΓΩΈΣΝΥ―–ΨΩΦ“”ΟΫΈ≥Β‘ΎΗΏΥΌΙΪ¬Ζ…œΒΡ≥ΒΥΌ«ιΩωΘ§ΫΜΆ®≤ΩΟ≈ΥφΜζΕ‘50ΟϊΦ“”ΟΫΈ≥ΒΦί Μ‘±Ϋχ––Βς≤ιΘ§ΒΟΒΫΤδ‘ΎΗΏΥΌΙΪ¬Ζ…œ–– Μ ±ΒΡΤΫΨυ≥ΒΥΌ«ιΩωΈΣΘΚ‘Ύ30ΟϊΡ––‘Φί Μ‘±÷–Θ§ΤΫΨυ≥ΒΥΌ≥§Ιΐ100km/hΒΡ”–20»ΥΘ§≤Μ≥§Ιΐ100km/hΒΡ”–10»ΥΘ°‘Ύ20Οϊ≈°–‘Φί Μ‘±÷–Θ§ΤΫΨυ≥ΒΥΌ≥§Ιΐ100km/hΒΡ”–5»ΥΘ§≤Μ≥§Ιΐ100km/hΒΡ”–15»ΥΘ°
Θ®ΔώΘ©Άξ≥…œ¬ΟφΒΡΝ–ΝΣ±μΘ§≤Δ≈–Εœ «Ζώ”–99.5%ΒΡΑ―Έ’»œΈΣΤΫΨυ≥ΒΥΌ≥§Ιΐ100km/hΒΡ»Υ”κ–‘±π”–ΙΊΘΜ
ΤΫΨυ≥ΒΥΌ≥§Ιΐ100km/h»Υ ΐ | ΤΫΨυ≥ΒΥΌ≤Μ≥§Ιΐ100km/h»Υ ΐ | ΚœΦΤ | |
Ρ––‘Φί Μ‘±»Υ ΐ | |||
≈°–‘Φί Μ‘±»Υ ΐ | |||
ΚœΦΤ | |||
Θ®ΔρΘ©“‘…œ ω ΐΨί―υ±Ψά¥ΙάΦΤΉήΧεΘ§œ÷¥”ΗΏΥΌΙΪ¬Ζ…œ–– ΜΒΡ¥σΝΩΦ“”ΟΫΈ≥Β÷–ΥφΜζ≥ι»Γ3ΝΨΘ§Φ«’β3ΝΨ≥Β÷–Φί Μ‘±ΈΣ≈°–‘«“≥ΒΥΌ≤Μ≥§Ιΐ100km/hΒΡ≥ΒΝΨ ΐΈΣΠΤΘ§»τΟΩ¥Έ≥ι»ΓΒΡΫαΙϊ «œύΜΞΕάΝΔΒΡΘ§«σΠΤΒΡΖ÷≤ΦΝ–ΚΆ ΐ―ßΤΎΆϊΘ°
≤ΈΩΦΙΪ ΫΘΚ ![]() Θ§Τδ÷–n=a+b+c+dΘ°
Θ§Τδ÷–n=a+b+c+dΘ°
≤ΈΩΦ ΐΨίΘΚ
PΘ®K2Γίk0Θ© | 0.150 | 0.100 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
ΓΨ¥πΑΗΓΩΫβΘΚΘ®ΔώΘ©ΗυΨίΧβ“βΘ§Χν–¥Ν–ΝΣ±μ»γœ¬ΘΜ
ΤΫΨυ≥Β ΐ≥§Ιΐ »Υ ΐ | ΤΫΨυ≥ΒΥΌ≤Μ≥§Ιΐ »Υ ΐ | ΚœΦΤ | |
Ρ––‘Φί Μ‘±»Υ ΐ | 20 | 10 | 30 |
≈°–‘Φί Μ‘±»Υ ΐ | 5 | 15 | 20 |
ΚœΦΤ | 25 | 25 | 50 |
ΦΤΥψK2= ![]() =
= ![]() Γ÷8.333ΘΨ7.879Θ§
Γ÷8.333ΘΨ7.879Θ§
Υυ“‘”–99.5%ΒΡΑ―Έ’»œΈΣΤΫΨυ≥ΒΥΌ≥§Ιΐ100km/h”κ–‘±π”–ΙΊΘΜ
Θ®ΔρΘ©ΗυΨί―υ±ΨΙάΦΤΉήΧεΒΡΥΦœκΘ§¥”ΗΏΥΌΙΪ¬Ζ…œ–– ΜΒΡ¥σΝΩΦ“”ΟΫΈ≥Β÷–ΥφΦ¥≥ι»Γ1ΝΨΘ§
Φί Μ‘±ΈΣ≈°–‘«“≥ΒΥΌ≤Μ≥§Ιΐ100km/hΒΡ≥ΒΝΨΒΡΗ≈¬ ΈΣ ![]() Θ§
Θ§
Υυ“‘ΠΈΒΡΩ…Ρή»Γ÷ΒΈΣ0Θ§1Θ§2Θ§3Θ§«“ΠΈΓΪBΘ®3Θ§ ![]() Θ©Θ§
Θ©Θ§
ΓύPΘ®ΠΈ=0Θ©= ![]()
![]()
![]() =
= ![]() Θ§
Θ§
PΘ®ΠΈ=1Θ©= ![]()
![]()
![]() =
= ![]() Θ§
Θ§
PΘ®ΠΈ=2Θ©= ![]()
![]()
![]() =
= ![]() Θ§
Θ§
PΘ®ΠΈ=3Θ©= ![]()
![]()
![]() =
= ![]() ΘΜ
ΘΜ
ΠΈΒΡΖ÷≤ΦΝ–ΈΣΘΚ
ΠΈ | 0 | 1 | 2 | 3 |
P | | | | |
ΐ―ßΤΎΆϊΈΣ ![]() ΘΜ
ΘΜ
Μρ ![]()
ΓΨΫβΈωΓΩΘ®ΔώΘ©ΗυΨίΧβ“βΘ§Χν–¥Ν–ΝΣ±μΘ§ΦΤΥψΙέ≤β÷ΒΘ§Ε‘’’ΝΌΫγ÷ΒΒΟ≥ωΫα¬έΘΜΘ®ΔρΘ©ΗυΨί―υ±ΨΙάΦΤΉήΧεΒΡΥΦœκΘ§«σΒΟ¥”ΗΏΥΌΙΪ¬Ζ…œ–– ΜΒΡ¥σΝΩΦ“”ΟΫΈ≥Β÷–ΥφΦ¥≥ι»Γ1ΝΨΘ§Φί Μ‘±ΈΣ≈°–‘«“≥ΒΥΌ≤Μ≥§Ιΐ100km/hΒΡ≥ΒΝΨΒΡΗ≈¬ Θ§÷ΣΠΈΒΡΩ…Ρή»Γ÷ΒΘ§«“ΠΈΓΪBΘ®3Θ§ ![]() Θ©Θ§
Θ©Θ§
ΦΤΥψΕ‘”ΠΒΡΗ≈¬ Θ§–¥≥ωΠΈΒΡΖ÷≤ΦΝ–Θ§ΦΤΥψ ΐ―ßΤΎΆϊ÷ΒΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΒ»≤ν ΐΝ–{an}ΒΡ«ΑnœνΚΆΈΣSn Θ§ a1=aΘ§Β±nΓί2 ±Θ§ ![]() =3n2an+S
=3n2an+S ![]() Θ§anΓΌ0Θ§nΓ N*Θ°
Θ§anΓΌ0Θ§nΓ N*Θ°
Θ®1Θ©«σaΒΡ÷ΒΘΜ
Θ®2Θ©…η ΐΝ–{cn}ΒΡ«ΑnœνΚΆΈΣTn Θ§ «“cn=3n©¹1+a5 Θ§ «σ Ι≤ΜΒ» Ϋ4TnΘΨS10≥…ΝΔΒΡΉν–Γ’ΐ’ϊ ΐnΒΡ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΥΡάβΉΕP©¹ABCDΒΡΒΉΟφ «“ΜΗω’ΐΖΫ–ΈΘ§PAΓΆΤΫΟφABCDΘ§PA=AB=2Θ§E «άβPAΒΡ÷–ΒψΘ§‘ρ“λΟφ÷±œΏBE”κACΥυ≥…Ϋ«ΒΡ”ύœ“÷Β «Θ® Θ© 
A.![]()
B.![]()
C.![]()
D.![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈΣΝΥ’Ι Ψ÷–ΜΣΚΚΉ÷ΒΡΈό«νς»ΝΠΘ§¥ΪΒί¥ΪΆ≥ΈΡΜ·Θ§ΧαΗΏ―ßœΑ»»«ιΘ§Ρ≥–ΘΩΣ’ΙΓΕ÷–ΙζΚΚΉ÷Χΐ–¥¥σΜαΓΖΒΡΜνΕ·Θ°ΈΣœλ”Π―ß–ΘΚ≈’ΌΘ§2Θ®9Θ©ΑύΉιΫ®ΝΥ–Υ»ΛΑύΘ§ΗυΨίΦΉΓΔ““ΝΫ»ΥΫϋΤΎ8¥Έ≥…Φ®Μ≠≥ωΨΞ“ΕΆΦΘ§»γΆΦΥυ ΨΘ®Α―ΤΒ¬ Β±ΉςΗ≈¬ Θ©Θ°

Θ®1Θ©«σΦΉΓΔ““ΝΫ»Υ≥…Φ®ΒΡΤΫΨυ ΐΚΆ÷–ΈΜ ΐΘΜ
Θ®2Θ©œ÷“Σ¥”ΦΉΓΔ““ΝΫ»Υ÷–―Γ≈…“Μ»Υ≤ΈΦ”±»»ϋΘ§¥”Ά≥ΦΤ―ßΒΡΫ«Ε»Θ§Ρψ»œΈΣ≈…ΡΡΈΜ―ß…ζ≤ΈΦ”±»ΫœΚœ ΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐfΘ®xΘ©=|x©¹1|©¹2|x+1|ΒΡΉν¥σ÷ΒΈΣkΘ°
Θ®1Θ©«σkΒΡ÷ΒΘΜ
Θ®2Θ©»τaΘ§bΘ§cΓ RΘ§ ![]() Θ§«σbΘ®a+cΘ©ΒΡΉν¥σ÷ΒΘ°
Θ§«σbΘ®a+cΘ©ΒΡΉν¥σ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥÷–―ßΥφΜζ―Γ»ΓΝΥ![]() ΟϊΡ–…ζΘ§ΫΪΥϊΟ«ΒΡ…μΗΏΉςΈΣ―υ±ΨΫχ––Ά≥ΦΤΘ§ΒΟΒΫ»γΆΦΥυ ΨΒΡΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘ§Ιέ≤λΆΦ÷– ΐΨίΘ§Άξ≥…œ¬Ν–Έ ΧβΘ°
ΟϊΡ–…ζΘ§ΫΪΥϊΟ«ΒΡ…μΗΏΉςΈΣ―υ±ΨΫχ––Ά≥ΦΤΘ§ΒΟΒΫ»γΆΦΥυ ΨΒΡΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘ§Ιέ≤λΆΦ÷– ΐΨίΘ§Άξ≥…œ¬Ν–Έ ΧβΘ°
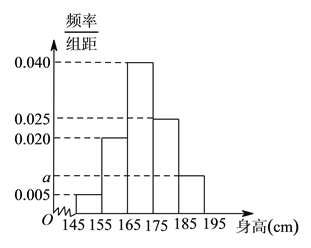
Θ®![]() Θ©«σ
Θ©«σ![]() ΒΡ÷ΒΦΑ―υ±Ψ÷–Ρ–…ζ…μΗΏ‘Ύ
ΒΡ÷ΒΦΑ―υ±Ψ÷–Ρ–…ζ…μΗΏ‘Ύ![]() Θ®ΒΞΈΜΘΚ
Θ®ΒΞΈΜΘΚ![]() Θ©ΒΡ»Υ ΐΘ°
Θ©ΒΡ»Υ ΐΘ°
Θ®![]() Θ©ΦΌ…η”Ο“ΜΉι÷–ΒΡΟΩΗω ΐΨίΩ…”ΟΗΟΉι«χΦδΒΡ÷–Βψ÷Β¥ζΧφΘ§Ά®Ιΐ―υ±ΨΙάΦΤΗΟ–Θ»ΪΧεΡ–…ζΒΡΤΫΨυ…μΗΏΘ°
Θ©ΦΌ…η”Ο“ΜΉι÷–ΒΡΟΩΗω ΐΨίΩ…”ΟΗΟΉι«χΦδΒΡ÷–Βψ÷Β¥ζΧφΘ§Ά®Ιΐ―υ±ΨΙάΦΤΗΟ–Θ»ΪΧεΡ–…ζΒΡΤΫΨυ…μΗΏΘ°
Θ®![]() Θ©‘Ύ―υ±Ψ÷–Θ§¥”…μΗΏ‘Ύ
Θ©‘Ύ―υ±Ψ÷–Θ§¥”…μΗΏ‘Ύ![]() ΚΆ
ΚΆ![]() Θ®ΒΞΈΜΘΚ
Θ®ΒΞΈΜΘΚ![]() Θ©ΡΎΒΡΡ–…ζ÷–»Έ―ΓΝΫ»ΥΘ§«σ’βΝΫ»ΥΒΡ…μΗΏΕΦ≤ΜΒΆ”Ύ
Θ©ΡΎΒΡΡ–…ζ÷–»Έ―ΓΝΫ»ΥΘ§«σ’βΝΫ»ΥΒΡ…μΗΏΕΦ≤ΜΒΆ”Ύ![]() ΒΡΗ≈¬ Θ°
ΒΡΗ≈¬ Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ…η≈ΉΈοœΏCΘΚx2=2pyΘ®pΘΨ0Θ©ΒΡΫΙΒψΈΣFΘ§ΉΦœΏΈΣlΘ§AΓ CΘ§“―÷Σ“‘FΈΣ‘≤–ΡΘ§FAΈΣΑκΨΕΒΡ‘≤FΫΜl”ΎBΘ§DΝΫΒψΘΜ
Θ®1Θ©»τΓœBFD=90ΓψΘ§ΓςABDΒΡΟφΜΐΈΣ ![]() Θ§«σpΒΡ÷ΒΦΑ‘≤FΒΡΖΫ≥ΧΘΜ
Θ§«σpΒΡ÷ΒΦΑ‘≤FΒΡΖΫ≥ΧΘΜ
Θ®2Θ©»τAΘ§BΘ§F»ΐΒψ‘ΎΆ§“Μ÷±œΏm…œΘ§÷±œΏn”κmΤΫ––Θ§«“n”κC÷Μ”–“ΜΗωΙΪΙ≤ΒψΘ§«σΉχ±ξ‘≠ΒψΒΫmΘ§nΨύάκΒΡ±»÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΦΚ÷ΣΚ· ΐfΘ®xΘ© «Ε®“ε‘ΎR…œΒΡ≈ΦΚ· ΐΘ§fΘ®x+1Θ©ΈΣΤφΚ· ΐΘ§fΘ®0Θ©=0Θ§Β±xΓ Θ®0Θ§1] ±Θ§fΘ®xΘ©=log2xΘ§‘ρ‘Ύ«χΦδΘ®8Θ§9Θ©ΡΎ¬ζΉψΖΫfΘ®xΘ©≥ΧfΘ®xΘ©+2=fΘ® ![]() Θ©ΒΡ Β ΐxΈΣ Θ® Θ©
Θ©ΒΡ Β ΐxΈΣ Θ® Θ©
A.![]()
B.![]()
C.![]()
D.![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΓςABC÷–Θ§Ϋ«AΓΔBΓΔCΥυΕ‘ΒΡ±ΏΖ÷±πΈΣaΘ§bΘ§cΘ§«“ ![]() =
= ![]()
Θ®1Θ©«σA
Θ®2Θ©«σcosB+cosCΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com